Plot 2-5 way Venn diagrams

Ploting function of 2-5 way Venn diagrams from 'VENNset' objects or count set vectors. A useful feature is the possiblity to combine the counts from several Venn comparisons with the same number of label sets in a single Venn diagram.

vennPlot(x, mymain = "Venn Diagram", mysub = "default", setlabels = "default", yoffset = seq(0, 10, by = 0.34), ccol = rep(1, 31), colmode = 1, lcol = c("#FF0000", "#008B00", "#0000FF", "#FF00FF", "#CD8500"), lines = c("#FF0000", "#008B00", "#0000FF", "#FF00FF", "#CD8500"), mylwd = 3, diacol = 1, type = "ellipse", ccex = 1, lcex = 1, sepsplit = "_", ...)

Arguments

x

VENNset or list of VENNset objects. Alternatively, a vector of Venn counts or a list of vectors of Venn counts can be provided as input. If several Venn comparisons are provided in a list then their results are combined in a single Venn diagram, where the count sets are organized above each other.

mymain

Main title of plot.

mysub

Subtitle of plot. Default mysub="default" reports the number of unique items in all sets, as well as the number of unique items in each individual set, respectively.

setlabels

The argument setlabels allows to provide a vector of custom sample labels. However, assigning the proper names in the name slots of the initial setlist is preferred for tracking purposes.

yoffset

The results from several Venn comparisons can be combined in a single Venn diagram by assigning to x a list with several VENNsets or count vectors. The positonal offset of the count sets in the plot can be controlled with the yoffset argument. The argument setting colmode allows to assign different colors to each count set. For instance, with colmode=2 one can assign to ccol a color vector or a list, such as ccol=c("blue", "red") or ccol=list(1:8, 8:1).

ccol

Character or numeric vector to define colors of count values, e.g. ccol=c("black","black","red").

colmode

See argument yoffset.

lcol

Character or numeric vector to define colors of set labels, e.g. lcol=c("red", "green")

lines

Character or numeric vector to define colors of lines in plot.

mylwd

Defines line width of shapes used in plot.

diacol

See argument type.

type

Defines shapes used to plot 4-way Venn diagram. Default type="ellipse" uses ellipses. The setting type="circle" returns an incomplete 4-way Venn diagram as circles. This representation misses two overlap sectors, but is sometimes easier to navigate than the default ellipse version. The missing Venn intersects are reported below the Venn diagram. Their font color can be controled with the argument diacol.

ccex

Controls font size for count values.

lcex

Controls font size for set labels.

sepsplit

Character used to separate sample labels in Venn counts.

...

Additional arguments to pass on.

Value

Venn diagram plot.

References

See examples in 'The Electronic Journal of Combinatorics': http://www.combinatorics.org/files/Surveys/ds5/VennSymmExamples.html

Author

Thomas Girke

Note

The functions provided here are an extension of the Venn diagram resources on this site: http://manuals.bioinformatics.ucr.edu/home/R_BioCondManual#TOC-Venn-Diagrams

See also

overLapper, olBarplot

Examples

## Sample data
setlist <- list(A=sample(letters, 18), B=sample(letters, 16),
                C=sample(letters, 20), D=sample(letters, 22),
                E=sample(letters, 18), F=sample(letters, 22))

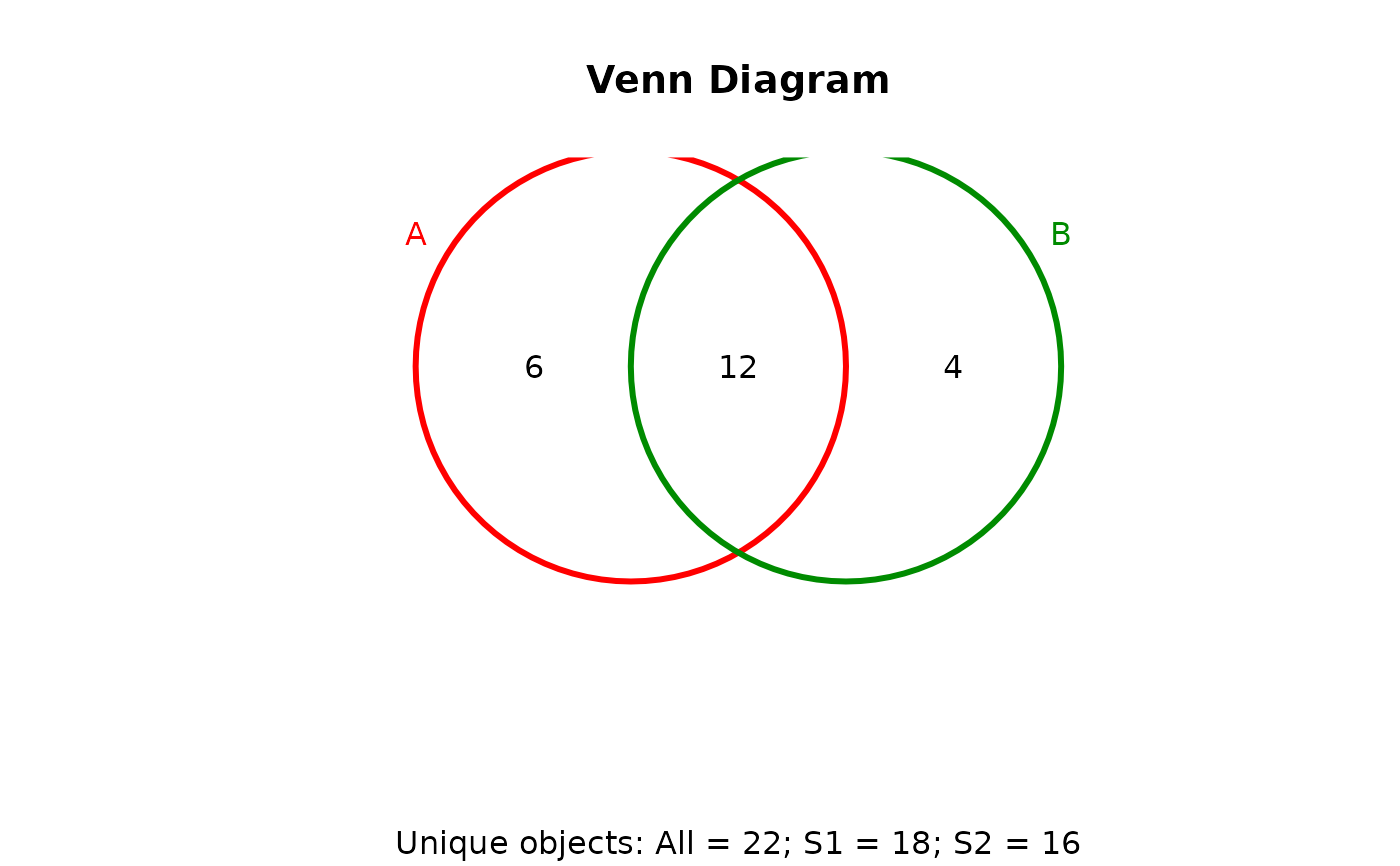
## 2-way Venn diagram
vennset <- overLapper(setlist[1:2], type="vennsets")
vennPlot(vennset)


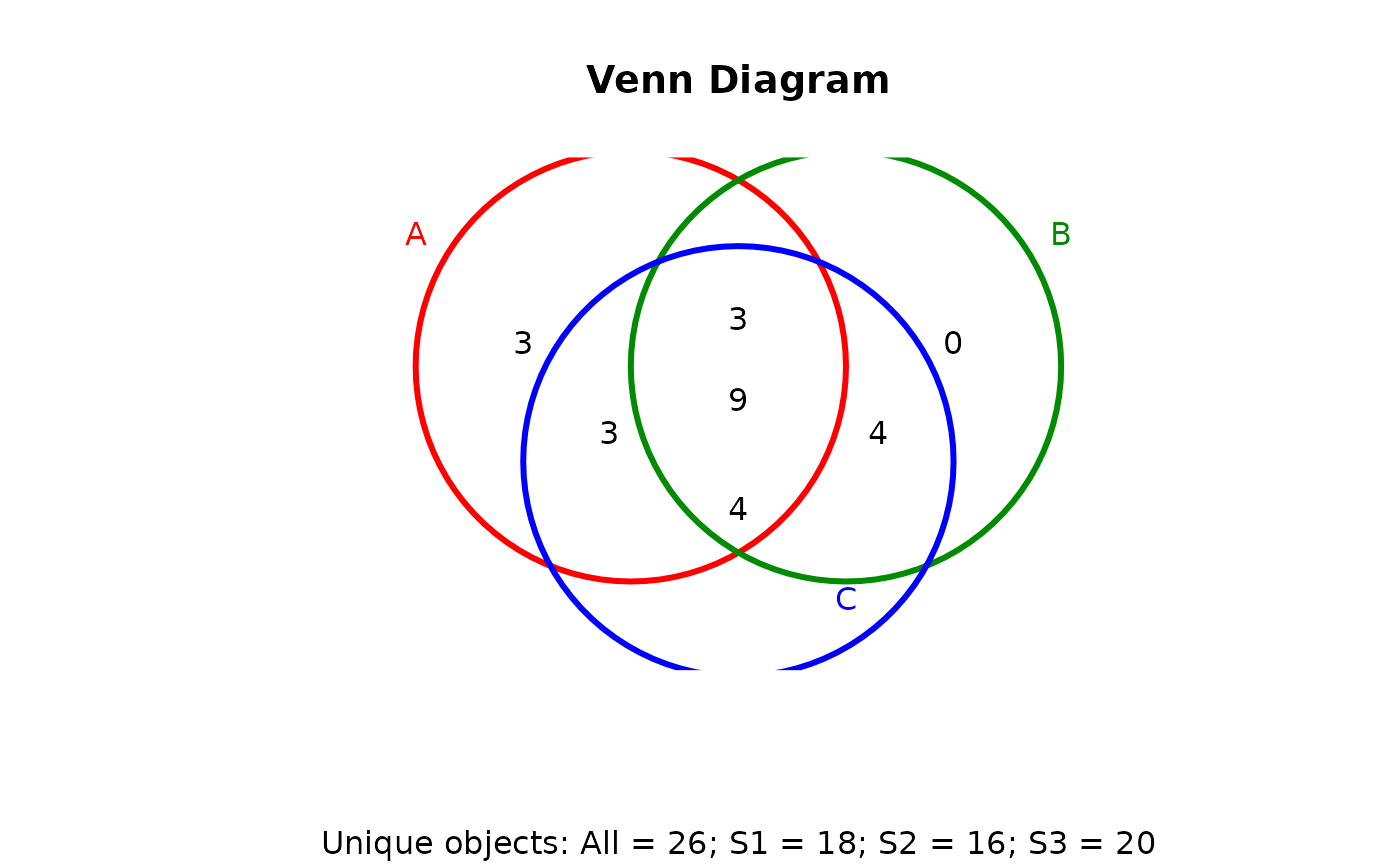
## 3-way Venn diagram
vennset <- overLapper(setlist[1:3], type="vennsets")
vennPlot(vennset)


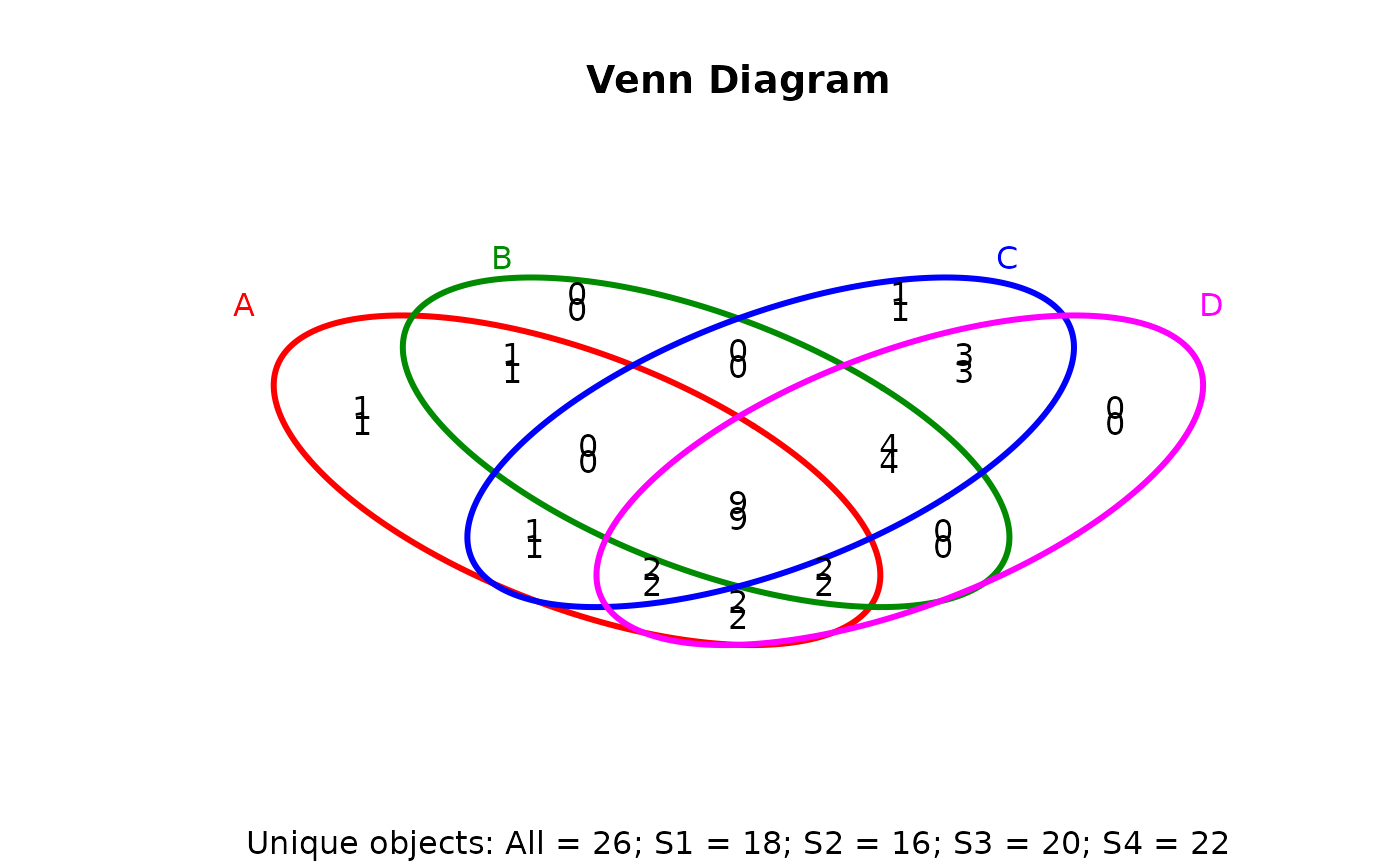
## 4-way Venn diagram
vennset <- overLapper(setlist[1:4], type="vennsets")
vennPlot(list(vennset, vennset))


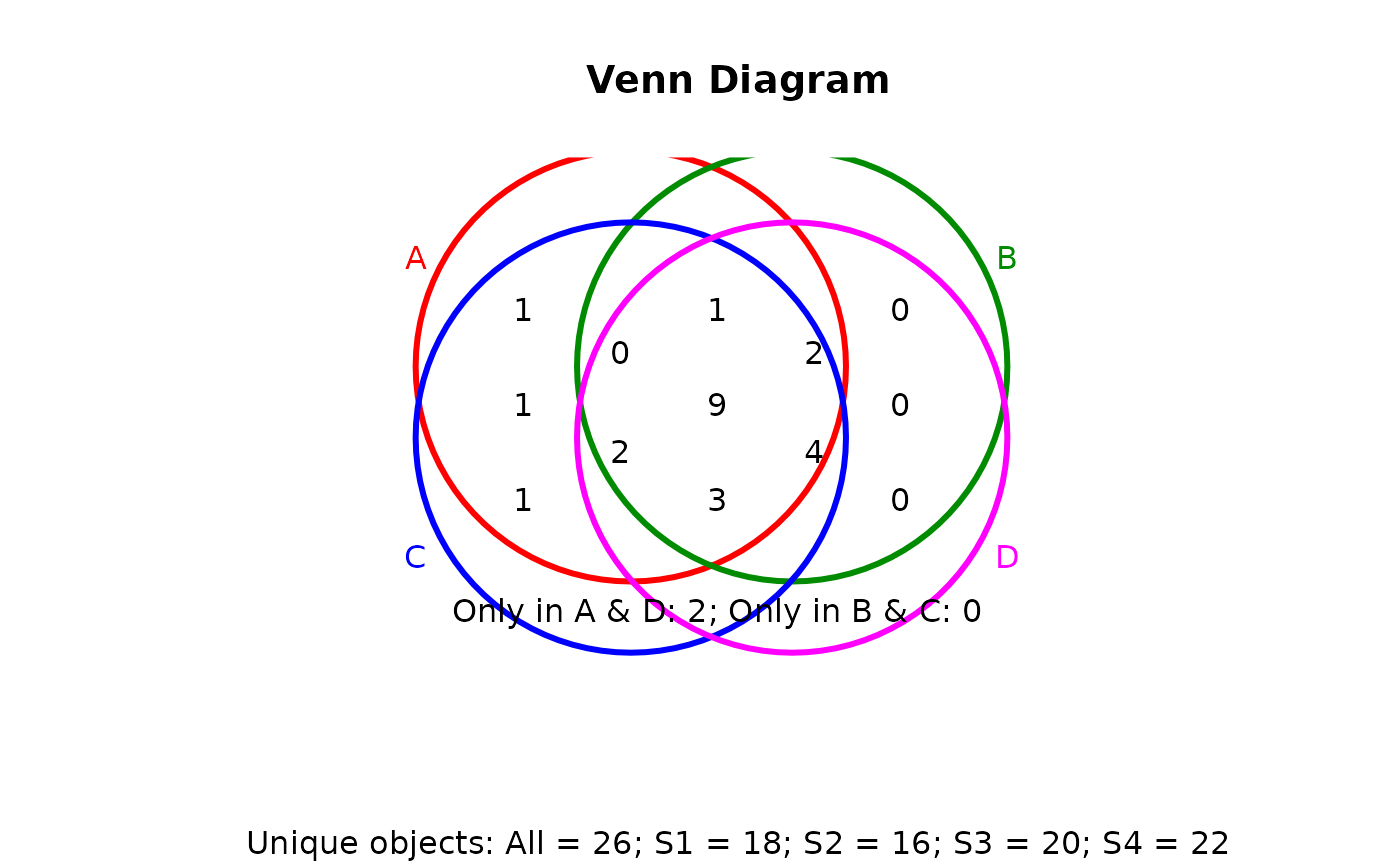
## Pseudo 4-way Venn diagram with circles
vennPlot(vennset, type="circle")


## 5-way Venn diagram
vennset <- overLapper(setlist[1:5], type="vennsets")
vennPlot(vennset)

## Alternative Venn count input to vennPlot (not recommended!)
counts <- sapply(vennlist(vennset), length)
vennPlot(counts)


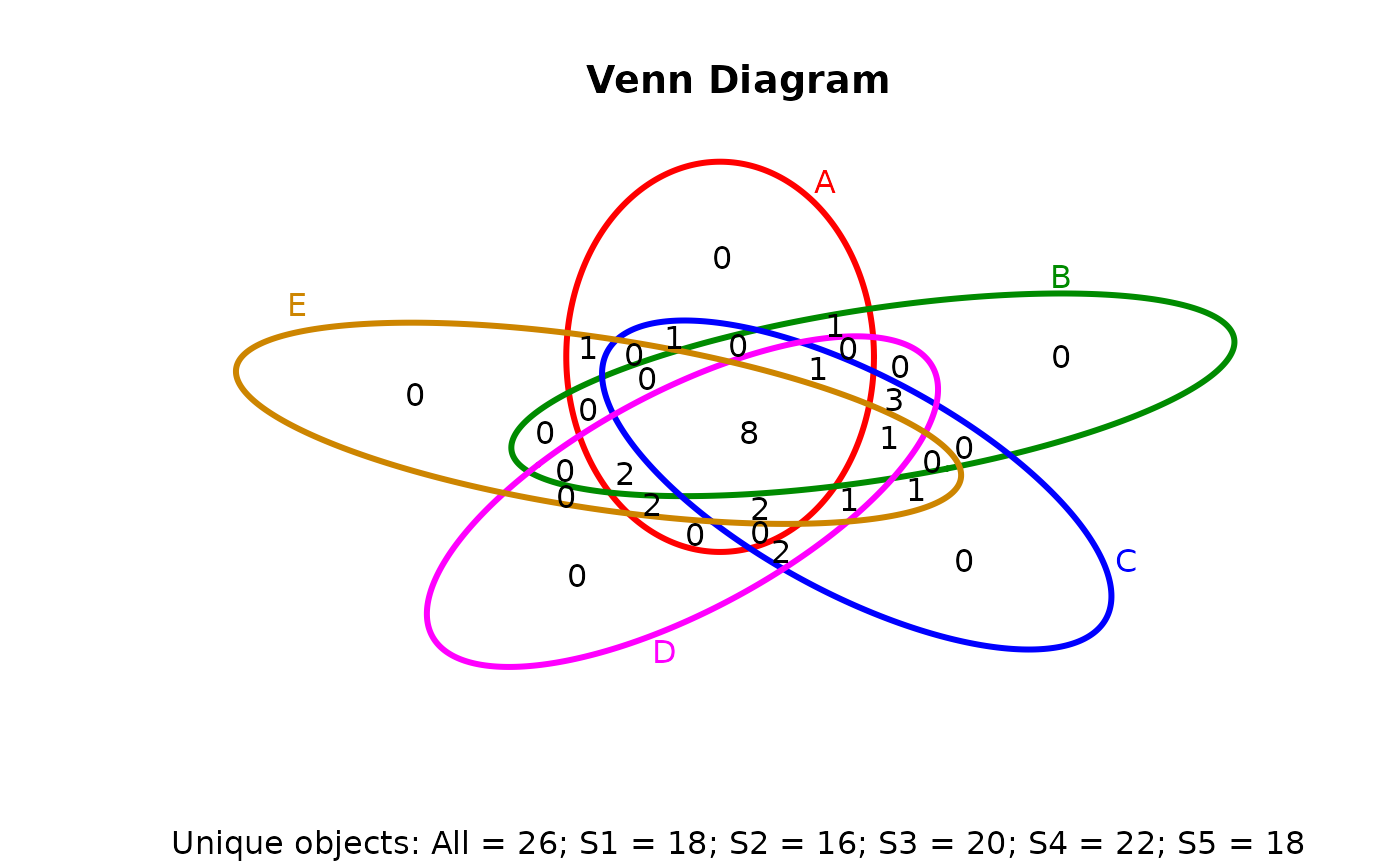## 6-way Venn comparison as bar plot
vennset <- overLapper(setlist[1:6], type="vennsets")
olBarplot(vennset, mincount=1)


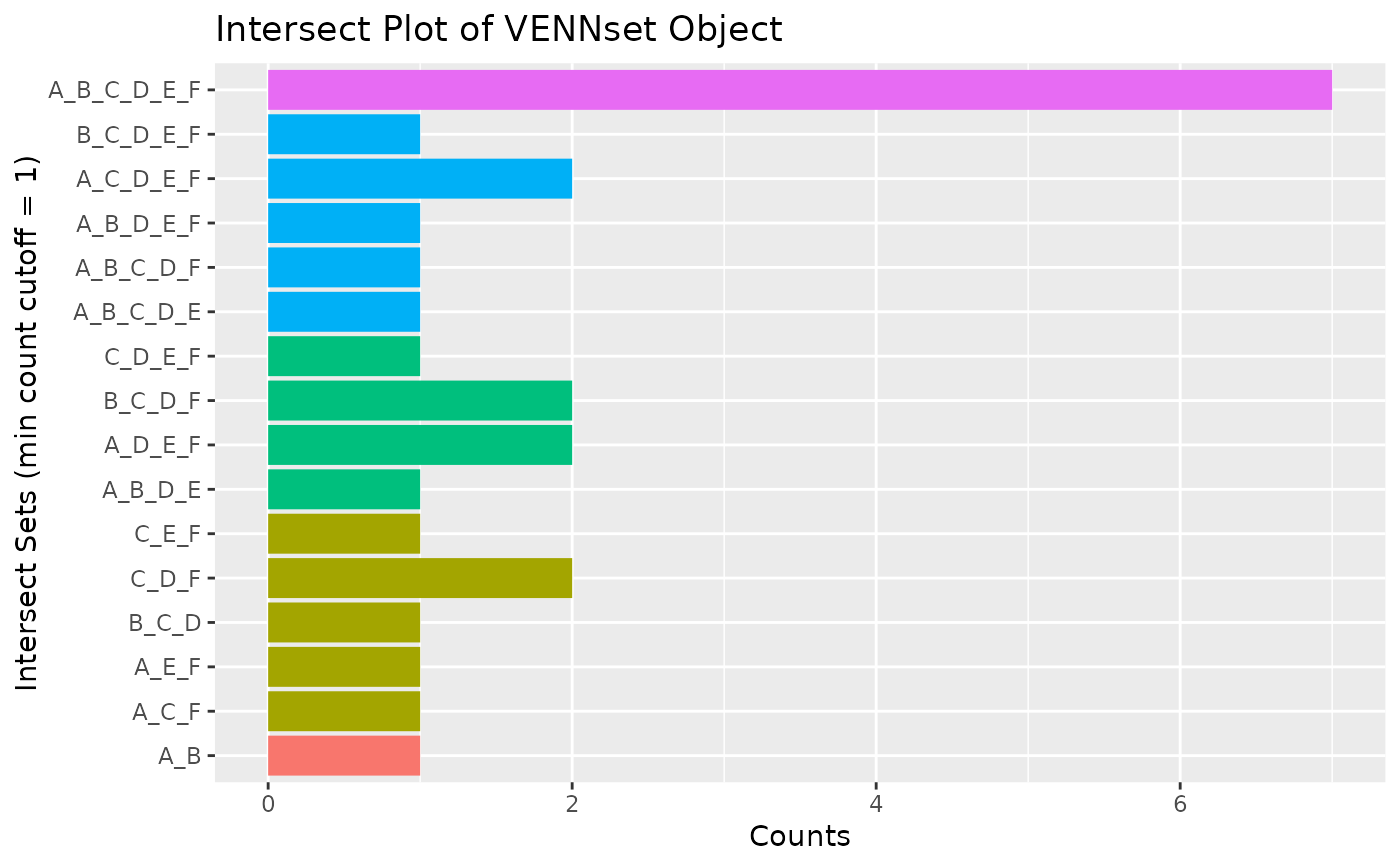## Bar plot of standard intersect counts
interset <- overLapper(setlist, type="intersects")
olBarplot(interset, mincount=1)


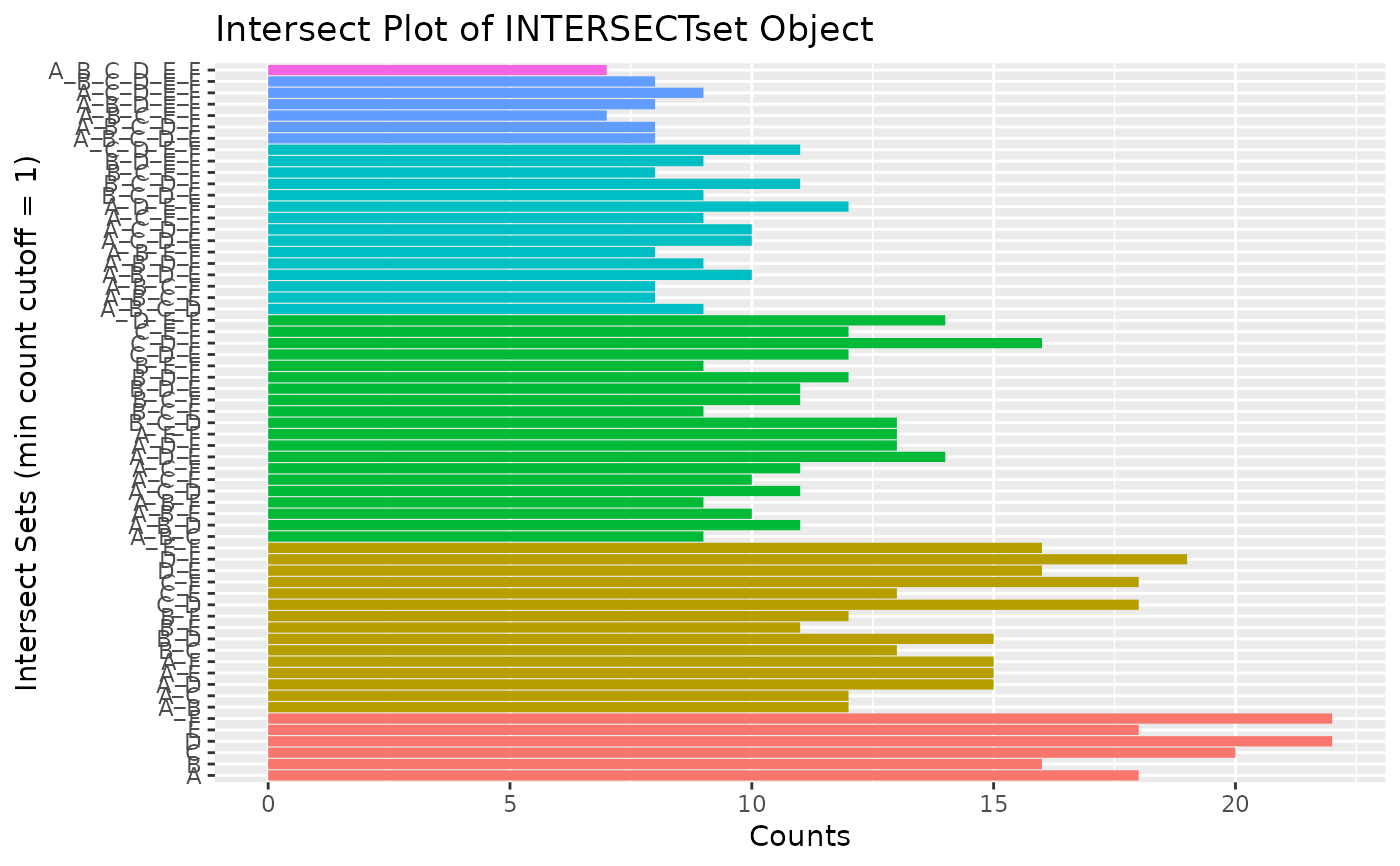## Accessor methods for VENNset/INTERSECTset objects
names(vennset)
#> [1] "setlist"          "intersectmatrix"  "complexitylevels" "vennlist"        
names(interset)
#> [1] "setlist"          "intersectmatrix"  "complexitylevels" "intersectlist"   
setlist(vennset)
#> $A
#>  [1] "h" "g" "r" "w" "s" "e" "x" "a" "l" "z" "u" "o" "c" "y" "q" "d" "v" "p"
#> 
#> $B
#>  [1] "d" "x" "p" "i" "h" "k" "g" "r" "z" "n" "s" "c" "q" "l" "y" "f"
#> 
#> $C
#>  [1] "z" "p" "g" "i" "s" "c" "f" "m" "q" "v" "u" "x" "b" "d" "h" "t" "w" "k" "j"
#> [20] "n"
#> 
#> $D
#>  [1] "j" "c" "n" "f" "t" "g" "d" "z" "i" "k" "h" "x" "w" "q" "e" "v" "s" "m" "l"
#> [20] "p" "o" "r"
#> 
#> $E
#>  [1] "d" "t" "v" "o" "a" "s" "z" "w" "h" "l" "n" "x" "b" "g" "c" "e" "r" "q"
#> 
#> $F
#>  [1] "e" "f" "w" "d" "l" "z" "m" "u" "t" "c" "p" "b" "s" "h" "i" "v" "j" "o" "x"
#> [20] "a" "q" "n"
#> 
intersectmatrix(vennset)
#>   A B C D E F
#> a 1 0 0 0 1 1
#> b 0 0 1 0 1 1
#> c 1 1 1 1 1 1
#> d 1 1 1 1 1 1
#> e 1 0 0 1 1 1
#> f 0 1 1 1 0 1
#> g 1 1 1 1 1 0
#> h 1 1 1 1 1 1
#> i 0 1 1 1 0 1
#> j 0 0 1 1 0 1
#> k 0 1 1 1 0 0
#> l 1 1 0 1 1 1
#> m 0 0 1 1 0 1
#> n 0 1 1 1 1 1
#> o 1 0 0 1 1 1
#> p 1 1 1 1 0 1
#> q 1 1 1 1 1 1
#> r 1 1 0 1 1 0
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 1
#> u 1 0 1 0 0 1
#> v 1 0 1 1 1 1
#> w 1 0 1 1 1 1
#> x 1 1 1 1 1 1
#> y 1 1 0 0 0 0
#> z 1 1 1 1 1 1
complexitylevels(vennset)
#>  [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
vennlist(vennset)
#> $A
#> character(0)
#> 
#> $B
#> character(0)
#> 
#> $C
#> character(0)
#> 
#> $D
#> character(0)
#> 
#> $E
#> character(0)
#> 
#> $F
#> character(0)
#> 
#> $A_B
#> [1] "y"
#> 
#> $A_C
#> character(0)
#> 
#> $A_D
#> character(0)
#> 
#> $A_E
#> character(0)
#> 
#> $A_F
#> character(0)
#> 
#> $B_C
#> character(0)
#> 
#> $B_D
#> character(0)
#> 
#> $B_E
#> character(0)
#> 
#> $B_F
#> character(0)
#> 
#> $C_D
#> character(0)
#> 
#> $C_E
#> character(0)
#> 
#> $C_F
#> character(0)
#> 
#> $D_E
#> character(0)
#> 
#> $D_F
#> character(0)
#> 
#> $E_F
#> character(0)
#> 
#> $A_B_C
#> character(0)
#> 
#> $A_B_D
#> character(0)
#> 
#> $A_B_E
#> character(0)
#> 
#> $A_B_F
#> character(0)
#> 
#> $A_C_D
#> character(0)
#> 
#> $A_C_E
#> character(0)
#> 
#> $A_C_F
#> [1] "u"
#> 
#> $A_D_E
#> character(0)
#> 
#> $A_D_F
#> character(0)
#> 
#> $A_E_F
#> [1] "a"
#> 
#> $B_C_D
#> [1] "k"
#> 
#> $B_C_E
#> character(0)
#> 
#> $B_C_F
#> character(0)
#> 
#> $B_D_E
#> character(0)
#> 
#> $B_D_F
#> character(0)
#> 
#> $B_E_F
#> character(0)
#> 
#> $C_D_E
#> character(0)
#> 
#> $C_D_F
#> [1] "j" "m"
#> 
#> $C_E_F
#> [1] "b"
#> 
#> $D_E_F
#> character(0)
#> 
#> $A_B_C_D
#> character(0)
#> 
#> $A_B_C_E
#> character(0)
#> 
#> $A_B_C_F
#> character(0)
#> 
#> $A_B_D_E
#> [1] "r"
#> 
#> $A_B_D_F
#> character(0)
#> 
#> $A_B_E_F
#> character(0)
#> 
#> $A_C_D_E
#> character(0)
#> 
#> $A_C_D_F
#> character(0)
#> 
#> $A_C_E_F
#> character(0)
#> 
#> $A_D_E_F
#> [1] "e" "o"
#> 
#> $B_C_D_E
#> character(0)
#> 
#> $B_C_D_F
#> [1] "f" "i"
#> 
#> $B_C_E_F
#> character(0)
#> 
#> $B_D_E_F
#> character(0)
#> 
#> $C_D_E_F
#> [1] "t"
#> 
#> $A_B_C_D_E
#> [1] "g"
#> 
#> $A_B_C_D_F
#> [1] "p"
#> 
#> $A_B_C_E_F
#> character(0)
#> 
#> $A_B_D_E_F
#> [1] "l"
#> 
#> $A_C_D_E_F
#> [1] "v" "w"
#> 
#> $B_C_D_E_F
#> [1] "n"
#> 
#> $A_B_C_D_E_F
#> [1] "c" "d" "h" "q" "s" "x" "z"
#> 
intersectlist(interset)
#> $A
#>  [1] "a" "c" "d" "e" "g" "h" "l" "o" "p" "q" "r" "s" "u" "v" "w" "x" "y" "z"
#> 
#> $B
#>  [1] "c" "d" "f" "g" "h" "i" "k" "l" "n" "p" "q" "r" "s" "x" "y" "z"
#> 
#> $C
#>  [1] "b" "c" "d" "f" "g" "h" "i" "j" "k" "m" "n" "p" "q" "s" "t" "u" "v" "w" "x"
#> [20] "z"
#> 
#> $D
#>  [1] "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "v"
#> [20] "w" "x" "z"
#> 
#> $E
#>  [1] "a" "b" "c" "d" "e" "g" "h" "l" "n" "o" "q" "r" "s" "t" "v" "w" "x" "z"
#> 
#> $F
#>  [1] "a" "b" "c" "d" "e" "f" "h" "i" "j" "l" "m" "n" "o" "p" "q" "s" "t" "u" "v"
#> [20] "w" "x" "z"
#> 
#> $A_B
#>  [1] "c" "d" "g" "h" "l" "p" "q" "r" "s" "x" "y" "z"
#> 
#> $A_C
#>  [1] "c" "d" "g" "h" "p" "q" "s" "u" "v" "w" "x" "z"
#> 
#> $A_D
#>  [1] "c" "d" "e" "g" "h" "l" "o" "p" "q" "r" "s" "v" "w" "x" "z"
#> 
#> $A_E
#>  [1] "a" "c" "d" "e" "g" "h" "l" "o" "q" "r" "s" "v" "w" "x" "z"
#> 
#> $A_F
#>  [1] "a" "c" "d" "e" "h" "l" "o" "p" "q" "s" "u" "v" "w" "x" "z"
#> 
#> $B_C
#>  [1] "c" "d" "f" "g" "h" "i" "k" "n" "p" "q" "s" "x" "z"
#> 
#> $B_D
#>  [1] "c" "d" "f" "g" "h" "i" "k" "l" "n" "p" "q" "r" "s" "x" "z"
#> 
#> $B_E
#>  [1] "c" "d" "g" "h" "l" "n" "q" "r" "s" "x" "z"
#> 
#> $B_F
#>  [1] "c" "d" "f" "h" "i" "l" "n" "p" "q" "s" "x" "z"
#> 
#> $C_D
#>  [1] "c" "d" "f" "g" "h" "i" "j" "k" "m" "n" "p" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $C_E
#>  [1] "b" "c" "d" "g" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $C_F
#>  [1] "b" "c" "d" "f" "h" "i" "j" "m" "n" "p" "q" "s" "t" "u" "v" "w" "x" "z"
#> 
#> $D_E
#>  [1] "c" "d" "e" "g" "h" "l" "n" "o" "q" "r" "s" "t" "v" "w" "x" "z"
#> 
#> $D_F
#>  [1] "c" "d" "e" "f" "h" "i" "j" "l" "m" "n" "o" "p" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $E_F
#>  [1] "a" "b" "c" "d" "e" "h" "l" "n" "o" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $A_B_C
#> [1] "c" "d" "g" "h" "p" "q" "s" "x" "z"
#> 
#> $A_B_D
#>  [1] "c" "d" "g" "h" "l" "p" "q" "r" "s" "x" "z"
#> 
#> $A_B_E
#>  [1] "c" "d" "g" "h" "l" "q" "r" "s" "x" "z"
#> 
#> $A_B_F
#> [1] "c" "d" "h" "l" "p" "q" "s" "x" "z"
#> 
#> $A_C_D
#>  [1] "c" "d" "g" "h" "p" "q" "s" "v" "w" "x" "z"
#> 
#> $A_C_E
#>  [1] "c" "d" "g" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $A_C_F
#>  [1] "c" "d" "h" "p" "q" "s" "u" "v" "w" "x" "z"
#> 
#> $A_D_E
#>  [1] "c" "d" "e" "g" "h" "l" "o" "q" "r" "s" "v" "w" "x" "z"
#> 
#> $A_D_F
#>  [1] "c" "d" "e" "h" "l" "o" "p" "q" "s" "v" "w" "x" "z"
#> 
#> $A_E_F
#>  [1] "a" "c" "d" "e" "h" "l" "o" "q" "s" "v" "w" "x" "z"
#> 
#> $B_C_D
#>  [1] "c" "d" "f" "g" "h" "i" "k" "n" "p" "q" "s" "x" "z"
#> 
#> $B_C_E
#> [1] "c" "d" "g" "h" "n" "q" "s" "x" "z"
#> 
#> $B_C_F
#>  [1] "c" "d" "f" "h" "i" "n" "p" "q" "s" "x" "z"
#> 
#> $B_D_E
#>  [1] "c" "d" "g" "h" "l" "n" "q" "r" "s" "x" "z"
#> 
#> $B_D_F
#>  [1] "c" "d" "f" "h" "i" "l" "n" "p" "q" "s" "x" "z"
#> 
#> $B_E_F
#> [1] "c" "d" "h" "l" "n" "q" "s" "x" "z"
#> 
#> $C_D_E
#>  [1] "c" "d" "g" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $C_D_F
#>  [1] "c" "d" "f" "h" "i" "j" "m" "n" "p" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $C_E_F
#>  [1] "b" "c" "d" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $D_E_F
#>  [1] "c" "d" "e" "h" "l" "n" "o" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $A_B_C_D
#> [1] "c" "d" "g" "h" "p" "q" "s" "x" "z"
#> 
#> $A_B_C_E
#> [1] "c" "d" "g" "h" "q" "s" "x" "z"
#> 
#> $A_B_C_F
#> [1] "c" "d" "h" "p" "q" "s" "x" "z"
#> 
#> $A_B_D_E
#>  [1] "c" "d" "g" "h" "l" "q" "r" "s" "x" "z"
#> 
#> $A_B_D_F
#> [1] "c" "d" "h" "l" "p" "q" "s" "x" "z"
#> 
#> $A_B_E_F
#> [1] "c" "d" "h" "l" "q" "s" "x" "z"
#> 
#> $A_C_D_E
#>  [1] "c" "d" "g" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $A_C_D_F
#>  [1] "c" "d" "h" "p" "q" "s" "v" "w" "x" "z"
#> 
#> $A_C_E_F
#> [1] "c" "d" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $A_D_E_F
#>  [1] "c" "d" "e" "h" "l" "o" "q" "s" "v" "w" "x" "z"
#> 
#> $B_C_D_E
#> [1] "c" "d" "g" "h" "n" "q" "s" "x" "z"
#> 
#> $B_C_D_F
#>  [1] "c" "d" "f" "h" "i" "n" "p" "q" "s" "x" "z"
#> 
#> $B_C_E_F
#> [1] "c" "d" "h" "n" "q" "s" "x" "z"
#> 
#> $B_D_E_F
#> [1] "c" "d" "h" "l" "n" "q" "s" "x" "z"
#> 
#> $C_D_E_F
#>  [1] "c" "d" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $A_B_C_D_E
#> [1] "c" "d" "g" "h" "q" "s" "x" "z"
#> 
#> $A_B_C_D_F
#> [1] "c" "d" "h" "p" "q" "s" "x" "z"
#> 
#> $A_B_C_E_F
#> [1] "c" "d" "h" "q" "s" "x" "z"
#> 
#> $A_B_D_E_F
#> [1] "c" "d" "h" "l" "q" "s" "x" "z"
#> 
#> $A_C_D_E_F
#> [1] "c" "d" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $B_C_D_E_F
#> [1] "c" "d" "h" "n" "q" "s" "x" "z"
#> 
#> $A_B_C_D_E_F
#> [1] "c" "d" "h" "q" "s" "x" "z"
#> 

## Coerce VENNset/INTERSECTset object to list
as.list(vennset)
#> $setlist
#> $setlist$A
#>  [1] "h" "g" "r" "w" "s" "e" "x" "a" "l" "z" "u" "o" "c" "y" "q" "d" "v" "p"
#> 
#> $setlist$B
#>  [1] "d" "x" "p" "i" "h" "k" "g" "r" "z" "n" "s" "c" "q" "l" "y" "f"
#> 
#> $setlist$C
#>  [1] "z" "p" "g" "i" "s" "c" "f" "m" "q" "v" "u" "x" "b" "d" "h" "t" "w" "k" "j"
#> [20] "n"
#> 
#> $setlist$D
#>  [1] "j" "c" "n" "f" "t" "g" "d" "z" "i" "k" "h" "x" "w" "q" "e" "v" "s" "m" "l"
#> [20] "p" "o" "r"
#> 
#> $setlist$E
#>  [1] "d" "t" "v" "o" "a" "s" "z" "w" "h" "l" "n" "x" "b" "g" "c" "e" "r" "q"
#> 
#> $setlist$F
#>  [1] "e" "f" "w" "d" "l" "z" "m" "u" "t" "c" "p" "b" "s" "h" "i" "v" "j" "o" "x"
#> [20] "a" "q" "n"
#> 
#> 
#> $intersectmatrix
#>   A B C D E F
#> a 1 0 0 0 1 1
#> b 0 0 1 0 1 1
#> c 1 1 1 1 1 1
#> d 1 1 1 1 1 1
#> e 1 0 0 1 1 1
#> f 0 1 1 1 0 1
#> g 1 1 1 1 1 0
#> h 1 1 1 1 1 1
#> i 0 1 1 1 0 1
#> j 0 0 1 1 0 1
#> k 0 1 1 1 0 0
#> l 1 1 0 1 1 1
#> m 0 0 1 1 0 1
#> n 0 1 1 1 1 1
#> o 1 0 0 1 1 1
#> p 1 1 1 1 0 1
#> q 1 1 1 1 1 1
#> r 1 1 0 1 1 0
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 1
#> u 1 0 1 0 0 1
#> v 1 0 1 1 1 1
#> w 1 0 1 1 1 1
#> x 1 1 1 1 1 1
#> y 1 1 0 0 0 0
#> z 1 1 1 1 1 1
#> 
#> $complexitylevels
#>  [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
#> 
#> $vennlist
#> $vennlist$A
#> character(0)
#> 
#> $vennlist$B
#> character(0)
#> 
#> $vennlist$C
#> character(0)
#> 
#> $vennlist$D
#> character(0)
#> 
#> $vennlist$E
#> character(0)
#> 
#> $vennlist$F
#> character(0)
#> 
#> $vennlist$A_B
#> [1] "y"
#> 
#> $vennlist$A_C
#> character(0)
#> 
#> $vennlist$A_D
#> character(0)
#> 
#> $vennlist$A_E
#> character(0)
#> 
#> $vennlist$A_F
#> character(0)
#> 
#> $vennlist$B_C
#> character(0)
#> 
#> $vennlist$B_D
#> character(0)
#> 
#> $vennlist$B_E
#> character(0)
#> 
#> $vennlist$B_F
#> character(0)
#> 
#> $vennlist$C_D
#> character(0)
#> 
#> $vennlist$C_E
#> character(0)
#> 
#> $vennlist$C_F
#> character(0)
#> 
#> $vennlist$D_E
#> character(0)
#> 
#> $vennlist$D_F
#> character(0)
#> 
#> $vennlist$E_F
#> character(0)
#> 
#> $vennlist$A_B_C
#> character(0)
#> 
#> $vennlist$A_B_D
#> character(0)
#> 
#> $vennlist$A_B_E
#> character(0)
#> 
#> $vennlist$A_B_F
#> character(0)
#> 
#> $vennlist$A_C_D
#> character(0)
#> 
#> $vennlist$A_C_E
#> character(0)
#> 
#> $vennlist$A_C_F
#> [1] "u"
#> 
#> $vennlist$A_D_E
#> character(0)
#> 
#> $vennlist$A_D_F
#> character(0)
#> 
#> $vennlist$A_E_F
#> [1] "a"
#> 
#> $vennlist$B_C_D
#> [1] "k"
#> 
#> $vennlist$B_C_E
#> character(0)
#> 
#> $vennlist$B_C_F
#> character(0)
#> 
#> $vennlist$B_D_E
#> character(0)
#> 
#> $vennlist$B_D_F
#> character(0)
#> 
#> $vennlist$B_E_F
#> character(0)
#> 
#> $vennlist$C_D_E
#> character(0)
#> 
#> $vennlist$C_D_F
#> [1] "j" "m"
#> 
#> $vennlist$C_E_F
#> [1] "b"
#> 
#> $vennlist$D_E_F
#> character(0)
#> 
#> $vennlist$A_B_C_D
#> character(0)
#> 
#> $vennlist$A_B_C_E
#> character(0)
#> 
#> $vennlist$A_B_C_F
#> character(0)
#> 
#> $vennlist$A_B_D_E
#> [1] "r"
#> 
#> $vennlist$A_B_D_F
#> character(0)
#> 
#> $vennlist$A_B_E_F
#> character(0)
#> 
#> $vennlist$A_C_D_E
#> character(0)
#> 
#> $vennlist$A_C_D_F
#> character(0)
#> 
#> $vennlist$A_C_E_F
#> character(0)
#> 
#> $vennlist$A_D_E_F
#> [1] "e" "o"
#> 
#> $vennlist$B_C_D_E
#> character(0)
#> 
#> $vennlist$B_C_D_F
#> [1] "f" "i"
#> 
#> $vennlist$B_C_E_F
#> character(0)
#> 
#> $vennlist$B_D_E_F
#> character(0)
#> 
#> $vennlist$C_D_E_F
#> [1] "t"
#> 
#> $vennlist$A_B_C_D_E
#> [1] "g"
#> 
#> $vennlist$A_B_C_D_F
#> [1] "p"
#> 
#> $vennlist$A_B_C_E_F
#> character(0)
#> 
#> $vennlist$A_B_D_E_F
#> [1] "l"
#> 
#> $vennlist$A_C_D_E_F
#> [1] "v" "w"
#> 
#> $vennlist$B_C_D_E_F
#> [1] "n"
#> 
#> $vennlist$A_B_C_D_E_F
#> [1] "c" "d" "h" "q" "s" "x" "z"
#> 
#> 
as.list(interset)
#> $setlist
#> $setlist$A
#>  [1] "h" "g" "r" "w" "s" "e" "x" "a" "l" "z" "u" "o" "c" "y" "q" "d" "v" "p"
#> 
#> $setlist$B
#>  [1] "d" "x" "p" "i" "h" "k" "g" "r" "z" "n" "s" "c" "q" "l" "y" "f"
#> 
#> $setlist$C
#>  [1] "z" "p" "g" "i" "s" "c" "f" "m" "q" "v" "u" "x" "b" "d" "h" "t" "w" "k" "j"
#> [20] "n"
#> 
#> $setlist$D
#>  [1] "j" "c" "n" "f" "t" "g" "d" "z" "i" "k" "h" "x" "w" "q" "e" "v" "s" "m" "l"
#> [20] "p" "o" "r"
#> 
#> $setlist$E
#>  [1] "d" "t" "v" "o" "a" "s" "z" "w" "h" "l" "n" "x" "b" "g" "c" "e" "r" "q"
#> 
#> $setlist$F
#>  [1] "e" "f" "w" "d" "l" "z" "m" "u" "t" "c" "p" "b" "s" "h" "i" "v" "j" "o" "x"
#> [20] "a" "q" "n"
#> 
#> 
#> $intersectmatrix
#>   A B C D E F
#> a 1 0 0 0 1 1
#> b 0 0 1 0 1 1
#> c 1 1 1 1 1 1
#> d 1 1 1 1 1 1
#> e 1 0 0 1 1 1
#> f 0 1 1 1 0 1
#> g 1 1 1 1 1 0
#> h 1 1 1 1 1 1
#> i 0 1 1 1 0 1
#> j 0 0 1 1 0 1
#> k 0 1 1 1 0 0
#> l 1 1 0 1 1 1
#> m 0 0 1 1 0 1
#> n 0 1 1 1 1 1
#> o 1 0 0 1 1 1
#> p 1 1 1 1 0 1
#> q 1 1 1 1 1 1
#> r 1 1 0 1 1 0
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 1
#> u 1 0 1 0 0 1
#> v 1 0 1 1 1 1
#> w 1 0 1 1 1 1
#> x 1 1 1 1 1 1
#> y 1 1 0 0 0 0
#> z 1 1 1 1 1 1
#> 
#> $complexitylevels
#>  [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
#> 
#> $intersectlist
#> $intersectlist$A
#>  [1] "a" "c" "d" "e" "g" "h" "l" "o" "p" "q" "r" "s" "u" "v" "w" "x" "y" "z"
#> 
#> $intersectlist$B
#>  [1] "c" "d" "f" "g" "h" "i" "k" "l" "n" "p" "q" "r" "s" "x" "y" "z"
#> 
#> $intersectlist$C
#>  [1] "b" "c" "d" "f" "g" "h" "i" "j" "k" "m" "n" "p" "q" "s" "t" "u" "v" "w" "x"
#> [20] "z"
#> 
#> $intersectlist$D
#>  [1] "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "v"
#> [20] "w" "x" "z"
#> 
#> $intersectlist$E
#>  [1] "a" "b" "c" "d" "e" "g" "h" "l" "n" "o" "q" "r" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$F
#>  [1] "a" "b" "c" "d" "e" "f" "h" "i" "j" "l" "m" "n" "o" "p" "q" "s" "t" "u" "v"
#> [20] "w" "x" "z"
#> 
#> $intersectlist$A_B
#>  [1] "c" "d" "g" "h" "l" "p" "q" "r" "s" "x" "y" "z"
#> 
#> $intersectlist$A_C
#>  [1] "c" "d" "g" "h" "p" "q" "s" "u" "v" "w" "x" "z"
#> 
#> $intersectlist$A_D
#>  [1] "c" "d" "e" "g" "h" "l" "o" "p" "q" "r" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_E
#>  [1] "a" "c" "d" "e" "g" "h" "l" "o" "q" "r" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_F
#>  [1] "a" "c" "d" "e" "h" "l" "o" "p" "q" "s" "u" "v" "w" "x" "z"
#> 
#> $intersectlist$B_C
#>  [1] "c" "d" "f" "g" "h" "i" "k" "n" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$B_D
#>  [1] "c" "d" "f" "g" "h" "i" "k" "l" "n" "p" "q" "r" "s" "x" "z"
#> 
#> $intersectlist$B_E
#>  [1] "c" "d" "g" "h" "l" "n" "q" "r" "s" "x" "z"
#> 
#> $intersectlist$B_F
#>  [1] "c" "d" "f" "h" "i" "l" "n" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$C_D
#>  [1] "c" "d" "f" "g" "h" "i" "j" "k" "m" "n" "p" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$C_E
#>  [1] "b" "c" "d" "g" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$C_F
#>  [1] "b" "c" "d" "f" "h" "i" "j" "m" "n" "p" "q" "s" "t" "u" "v" "w" "x" "z"
#> 
#> $intersectlist$D_E
#>  [1] "c" "d" "e" "g" "h" "l" "n" "o" "q" "r" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$D_F
#>  [1] "c" "d" "e" "f" "h" "i" "j" "l" "m" "n" "o" "p" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$E_F
#>  [1] "a" "b" "c" "d" "e" "h" "l" "n" "o" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$A_B_C
#> [1] "c" "d" "g" "h" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_D
#>  [1] "c" "d" "g" "h" "l" "p" "q" "r" "s" "x" "z"
#> 
#> $intersectlist$A_B_E
#>  [1] "c" "d" "g" "h" "l" "q" "r" "s" "x" "z"
#> 
#> $intersectlist$A_B_F
#> [1] "c" "d" "h" "l" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$A_C_D
#>  [1] "c" "d" "g" "h" "p" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_C_E
#>  [1] "c" "d" "g" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_C_F
#>  [1] "c" "d" "h" "p" "q" "s" "u" "v" "w" "x" "z"
#> 
#> $intersectlist$A_D_E
#>  [1] "c" "d" "e" "g" "h" "l" "o" "q" "r" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_D_F
#>  [1] "c" "d" "e" "h" "l" "o" "p" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_E_F
#>  [1] "a" "c" "d" "e" "h" "l" "o" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$B_C_D
#>  [1] "c" "d" "f" "g" "h" "i" "k" "n" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$B_C_E
#> [1] "c" "d" "g" "h" "n" "q" "s" "x" "z"
#> 
#> $intersectlist$B_C_F
#>  [1] "c" "d" "f" "h" "i" "n" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$B_D_E
#>  [1] "c" "d" "g" "h" "l" "n" "q" "r" "s" "x" "z"
#> 
#> $intersectlist$B_D_F
#>  [1] "c" "d" "f" "h" "i" "l" "n" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$B_E_F
#> [1] "c" "d" "h" "l" "n" "q" "s" "x" "z"
#> 
#> $intersectlist$C_D_E
#>  [1] "c" "d" "g" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$C_D_F
#>  [1] "c" "d" "f" "h" "i" "j" "m" "n" "p" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$C_E_F
#>  [1] "b" "c" "d" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$D_E_F
#>  [1] "c" "d" "e" "h" "l" "n" "o" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$A_B_C_D
#> [1] "c" "d" "g" "h" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_C_E
#> [1] "c" "d" "g" "h" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_C_F
#> [1] "c" "d" "h" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_D_E
#>  [1] "c" "d" "g" "h" "l" "q" "r" "s" "x" "z"
#> 
#> $intersectlist$A_B_D_F
#> [1] "c" "d" "h" "l" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_E_F
#> [1] "c" "d" "h" "l" "q" "s" "x" "z"
#> 
#> $intersectlist$A_C_D_E
#>  [1] "c" "d" "g" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_C_D_F
#>  [1] "c" "d" "h" "p" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_C_E_F
#> [1] "c" "d" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$A_D_E_F
#>  [1] "c" "d" "e" "h" "l" "o" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$B_C_D_E
#> [1] "c" "d" "g" "h" "n" "q" "s" "x" "z"
#> 
#> $intersectlist$B_C_D_F
#>  [1] "c" "d" "f" "h" "i" "n" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$B_C_E_F
#> [1] "c" "d" "h" "n" "q" "s" "x" "z"
#> 
#> $intersectlist$B_D_E_F
#> [1] "c" "d" "h" "l" "n" "q" "s" "x" "z"
#> 
#> $intersectlist$C_D_E_F
#>  [1] "c" "d" "h" "n" "q" "s" "t" "v" "w" "x" "z"
#> 
#> $intersectlist$A_B_C_D_E
#> [1] "c" "d" "g" "h" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_C_D_F
#> [1] "c" "d" "h" "p" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_C_E_F
#> [1] "c" "d" "h" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_D_E_F
#> [1] "c" "d" "h" "l" "q" "s" "x" "z"
#> 
#> $intersectlist$A_C_D_E_F
#> [1] "c" "d" "h" "q" "s" "v" "w" "x" "z"
#> 
#> $intersectlist$B_C_D_E_F
#> [1] "c" "d" "h" "n" "q" "s" "x" "z"
#> 
#> $intersectlist$A_B_C_D_E_F
#> [1] "c" "d" "h" "q" "s" "x" "z"
#> 
#> 

## Pairwise intersect matrix and heatmap
olMA <- sapply(names(setlist), 
    function(x) sapply(names(setlist), 
    function(y) sum(setlist[[x]] %in% setlist[[y]])))
olMA
#>    A  B  C  D  E  F
#> A 18 12 12 15 15 15
#> B 12 16 13 15 11 12
#> C 12 13 20 18 13 18
#> D 15 15 18 22 16 19
#> E 15 11 13 16 18 16
#> F 15 12 18 19 16 22
heatmap(olMA, Rowv=NA, Colv=NA)


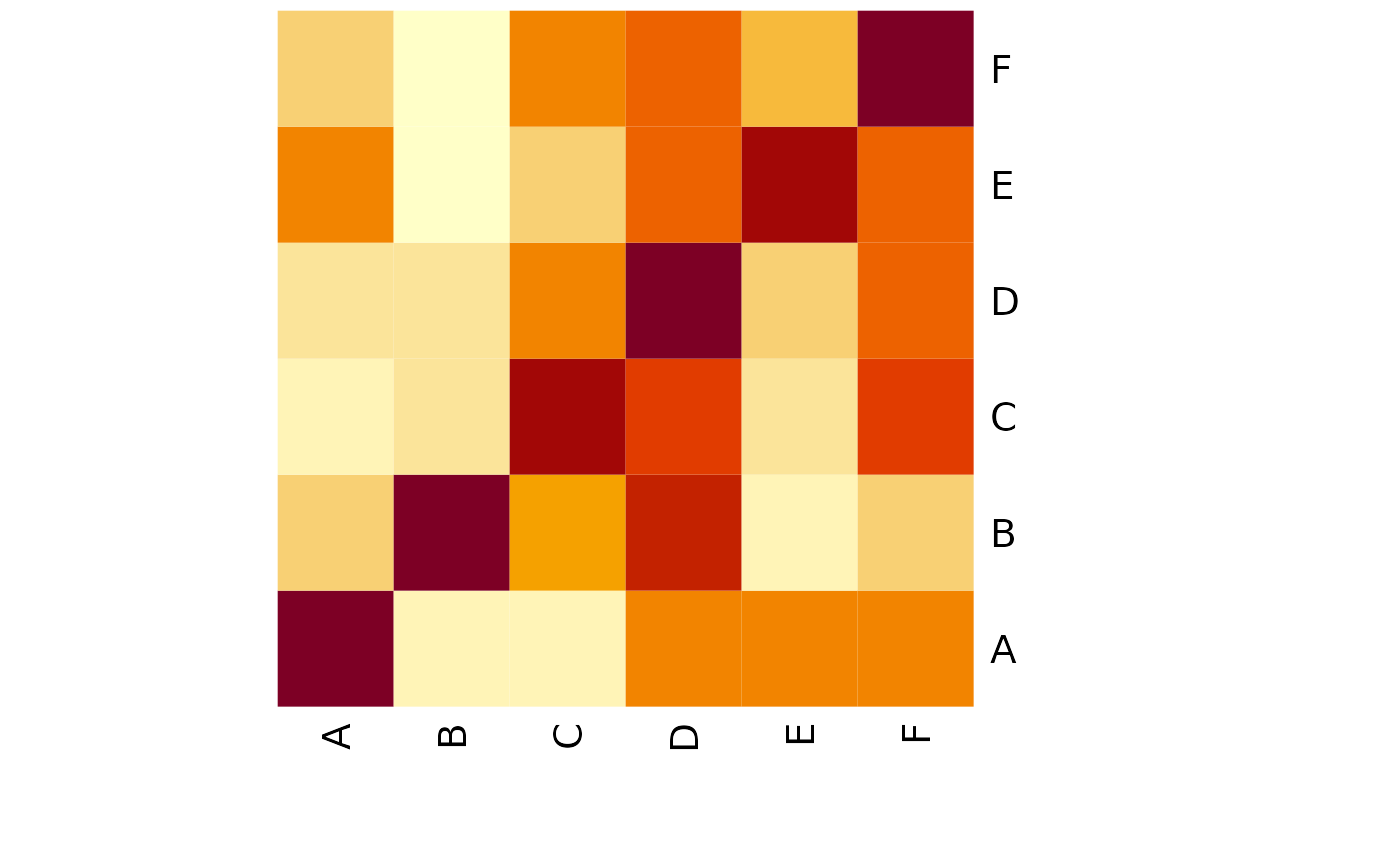## Presence-absence matrices for large numbers of sample sets
interset <- overLapper(setlist=setlist, type="intersects", complexity=2)
(paMA <- intersectmatrix(interset))
#>   A B C D E F
#> a 1 0 0 0 1 1
#> b 0 0 1 0 1 1
#> c 1 1 1 1 1 1
#> d 1 1 1 1 1 1
#> e 1 0 0 1 1 1
#> f 0 1 1 1 0 1
#> g 1 1 1 1 1 0
#> h 1 1 1 1 1 1
#> i 0 1 1 1 0 1
#> j 0 0 1 1 0 1
#> k 0 1 1 1 0 0
#> l 1 1 0 1 1 1
#> m 0 0 1 1 0 1
#> n 0 1 1 1 1 1
#> o 1 0 0 1 1 1
#> p 1 1 1 1 0 1
#> q 1 1 1 1 1 1
#> r 1 1 0 1 1 0
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 1
#> u 1 0 1 0 0 1
#> v 1 0 1 1 1 1
#> w 1 0 1 1 1 1
#> x 1 1 1 1 1 1
#> y 1 1 0 0 0 0
#> z 1 1 1 1 1 1
heatmap(paMA, Rowv=NA, Colv=NA, col=c("white", "gray"))