Set Intersect and Venn Diagram Functions
overLapper.RdFunction for computing Venn intersects or standard intersects among large
numbers of label sets provided as list of vectors. The resulting
intersect objects can be used for plotting 2-5 way Venn diagrams or intersect
bar plots using the functions vennPlot or olBarplot, respectively.
The overLapper function scales to 2-20 or more label vectors for Venn
intersect calculations and to much larger sample numbers for standard
intersects. The different intersect types are explained below under the
definition of the type argument. The upper Venn limit around 20 label
sets is unavoidable because the complexity of Venn intersects increases
exponentially with the label set number n according to this
relationship: 2^n - 1. The current implementation of
the plotting function vennPlot supports Venn diagrams for 2-5 label
sets. To visually analyze larger numbers of label sets, a variety of intersect
methods are introduced in the olBarplot help file. These methods are
much more scalable than Venn diagrams, but lack their restrictive intersect
logic.
overLapper(setlist, complexity = "default", sep = "_", cleanup = FALSE, keepdups = FALSE, type)Arguments
- setlist
Object of class
listwhere each list component stores a label set asvectorand the name of each label set is stored in the name slot of each list component. The names are used for naming the label sets in all downstream analysis steps and plots.- complexity
Complexity level of intersects specified as integer vector. For Venn intersects it needs to be assigned
1:length(setlist)(default). Ifcomplexity=2the function returns all pairwise intersects.- sep
Character used to separate set labels.
- cleanup
If set to
TRUEthen all characters of the label sets are set to upper case, and leading and trailing spaces are removed. The defaultcleanup=FALSEomits this step.- keepdups
By default all duplicates are removed from the label sets. The setting
keepdups=TRUEwill retain duplicates by appending a counter to each entry.- type
With the default setting
type="vennsets"the overLapper function computes the typical Venn intersects for the label sets provided undersetlist. With the settingtype="intersects"the function will compute pairwise intersects (not compatible with Venn diagrams). Venn intersects follow the typical 'only in' intersect logic of Venn comparisons, such as: labels present only in set A, labels present only in the intersect of A & B, etc. Due to this restrictive intersect logic, the combined Venn sets contain no duplicates. In contrast to this, regular intersects follow this logic: labels present in the intersect of A & B, labels present in the intersect of A & B & C, etc. This approach results usually in many duplications of labels among the intersect sets.
Details
Additional Venn diagram resources are provided by the packages limma,
gplots, vennerable, eVenn and VennDiagram, or
online resources such as shapes, Venn Diagram Generator and Venny.
Value
overLapper returns standard intersect and Venn intersect results as
INTERSECTset or VENNset objects, respectively. These S4 objects
contain the following components:
- setlist
Original label sets accessible with
setlist().- intersectmatrix
Present-absent matrix accessible with
intersectmatrix(), where each overlap set in thevennlistdata component is labeled according to the label set names provided undersetlist. For instance, the composite name 'ABC' indicates that the entries are restricted to A, B and C. The seperator used for naming the intersect sets can be specified under thesepargument.- complexitylevels
Complexity levels accessible with
complexitylevels().- vennlist
Venn intersects for
VENNsetobjects accessible withvennlist().- intersectlist
Standard intersects for
INTERSECTsetobjects accessible withintersectlist().
References
See examples in 'The Electronic Journal of Combinatorics': http://www.combinatorics.org/files/Surveys/ds5/VennSymmExamples.html
Note
The functions provided here are an extension of the Venn diagram resources on this site: http://manuals.bioinformatics.ucr.edu/home/R_BioCondManual#TOC-Venn-Diagrams
See also
vennPlot, olBarplot
Examples
## Sample data
setlist <- list(A=sample(letters, 18), B=sample(letters, 16),
C=sample(letters, 20), D=sample(letters, 22),
E=sample(letters, 18), F=sample(letters, 22))
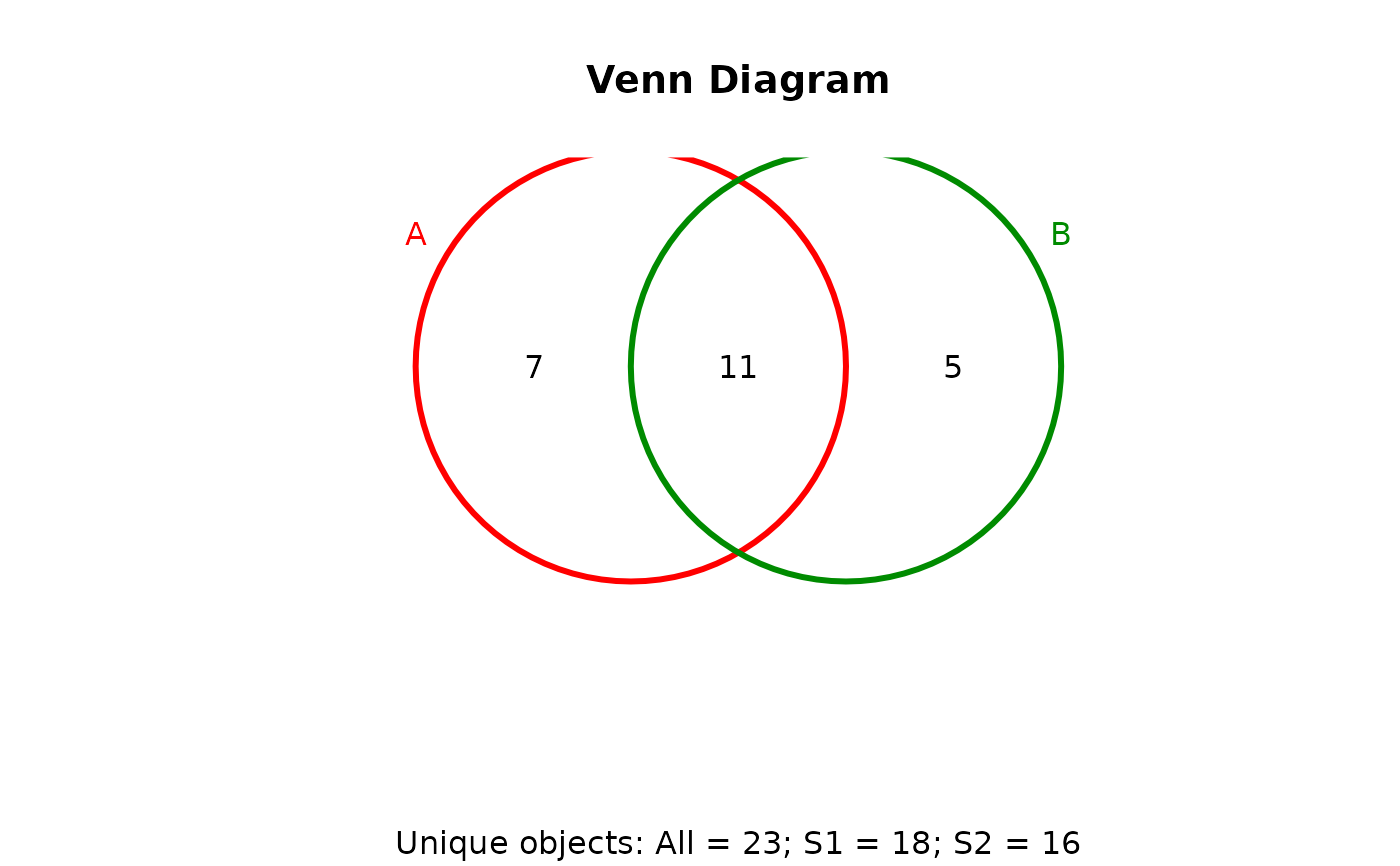
## 2-way Venn diagram
vennset <- overLapper(setlist[1:2], type="vennsets")
vennPlot(vennset)
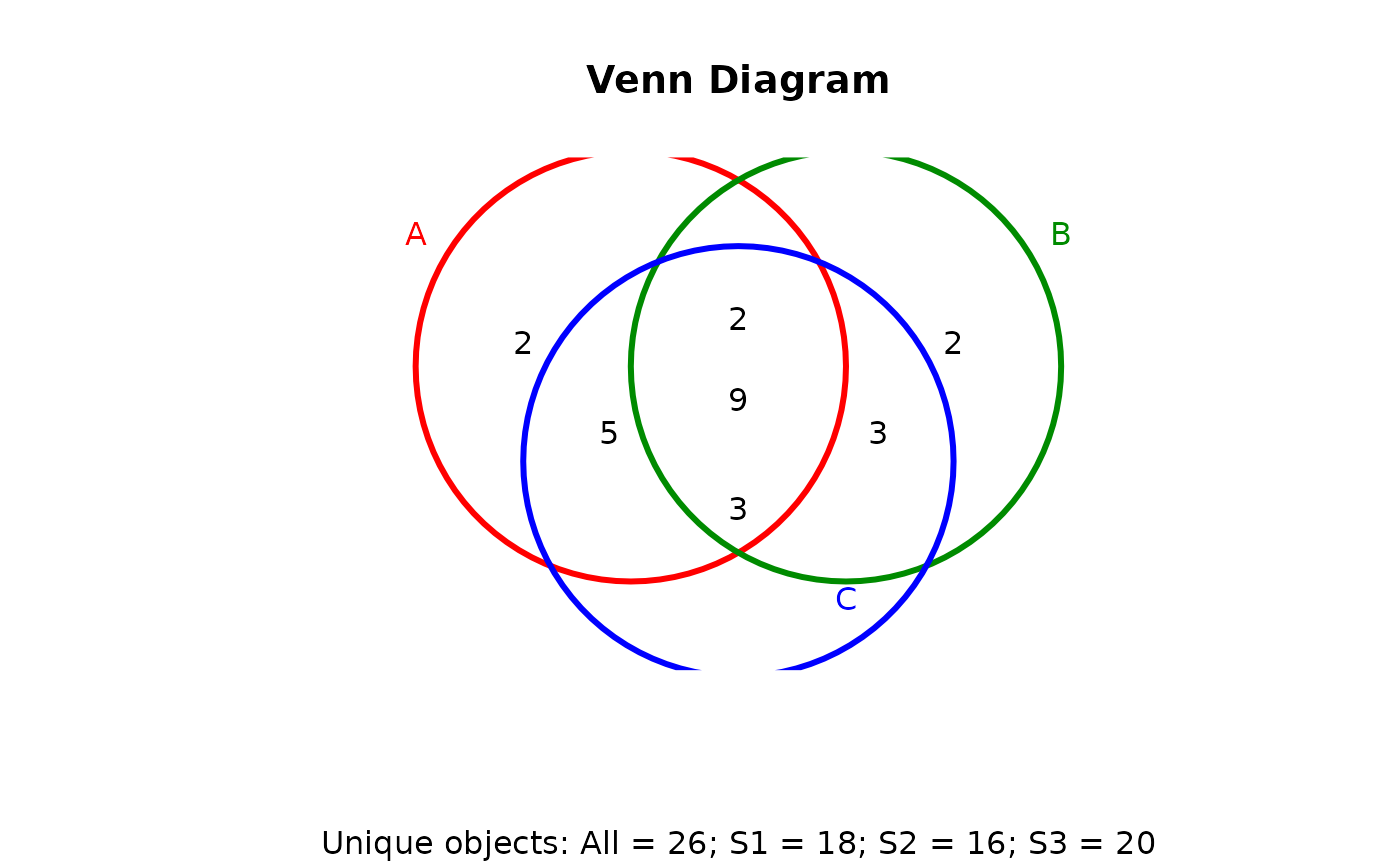
 ## 3-way Venn diagram
vennset <- overLapper(setlist[1:3], type="vennsets")
vennPlot(vennset)
## 3-way Venn diagram
vennset <- overLapper(setlist[1:3], type="vennsets")
vennPlot(vennset)
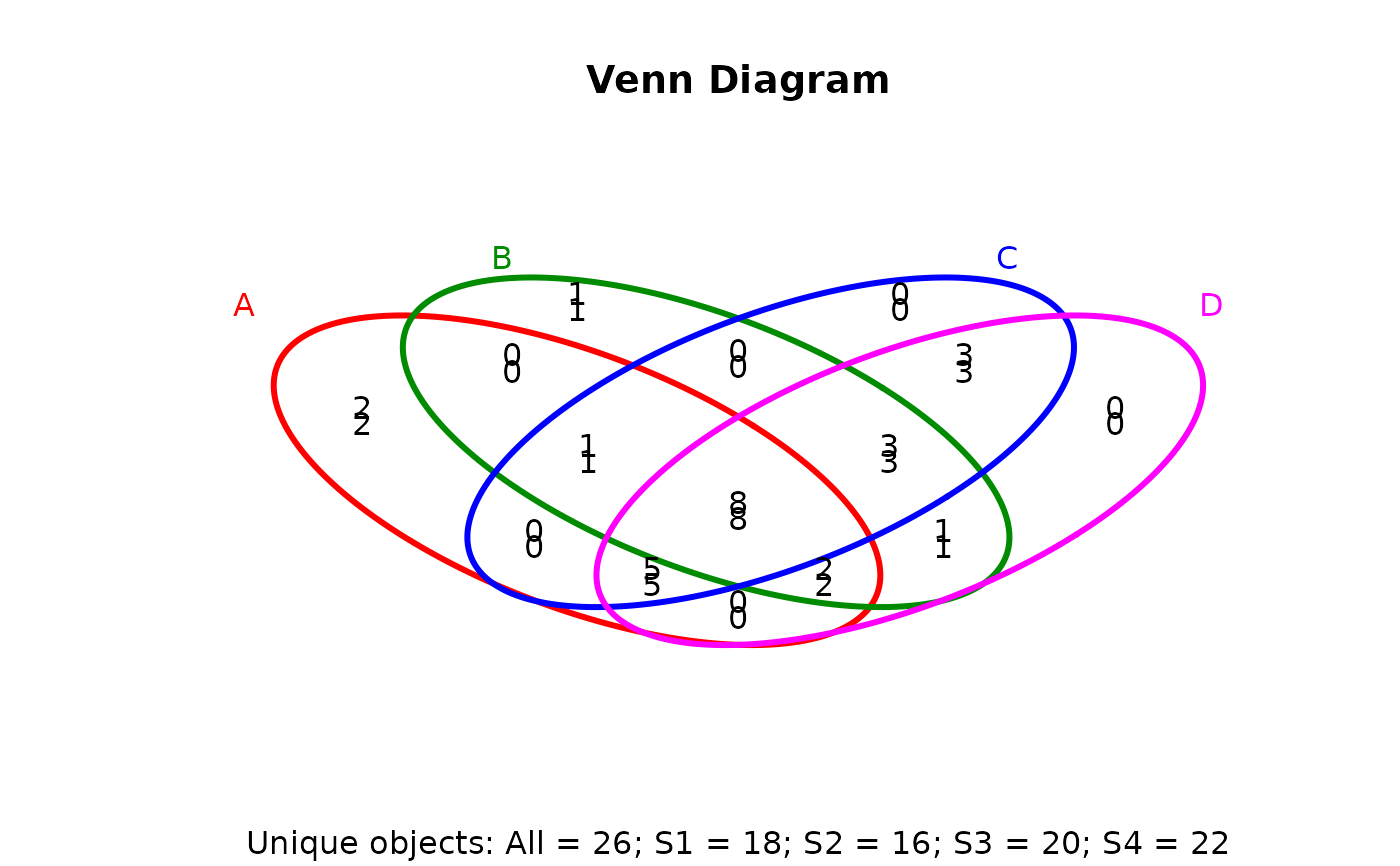
 ## 4-way Venn diagram
vennset <- overLapper(setlist[1:4], type="vennsets")
vennPlot(list(vennset, vennset))
## 4-way Venn diagram
vennset <- overLapper(setlist[1:4], type="vennsets")
vennPlot(list(vennset, vennset))
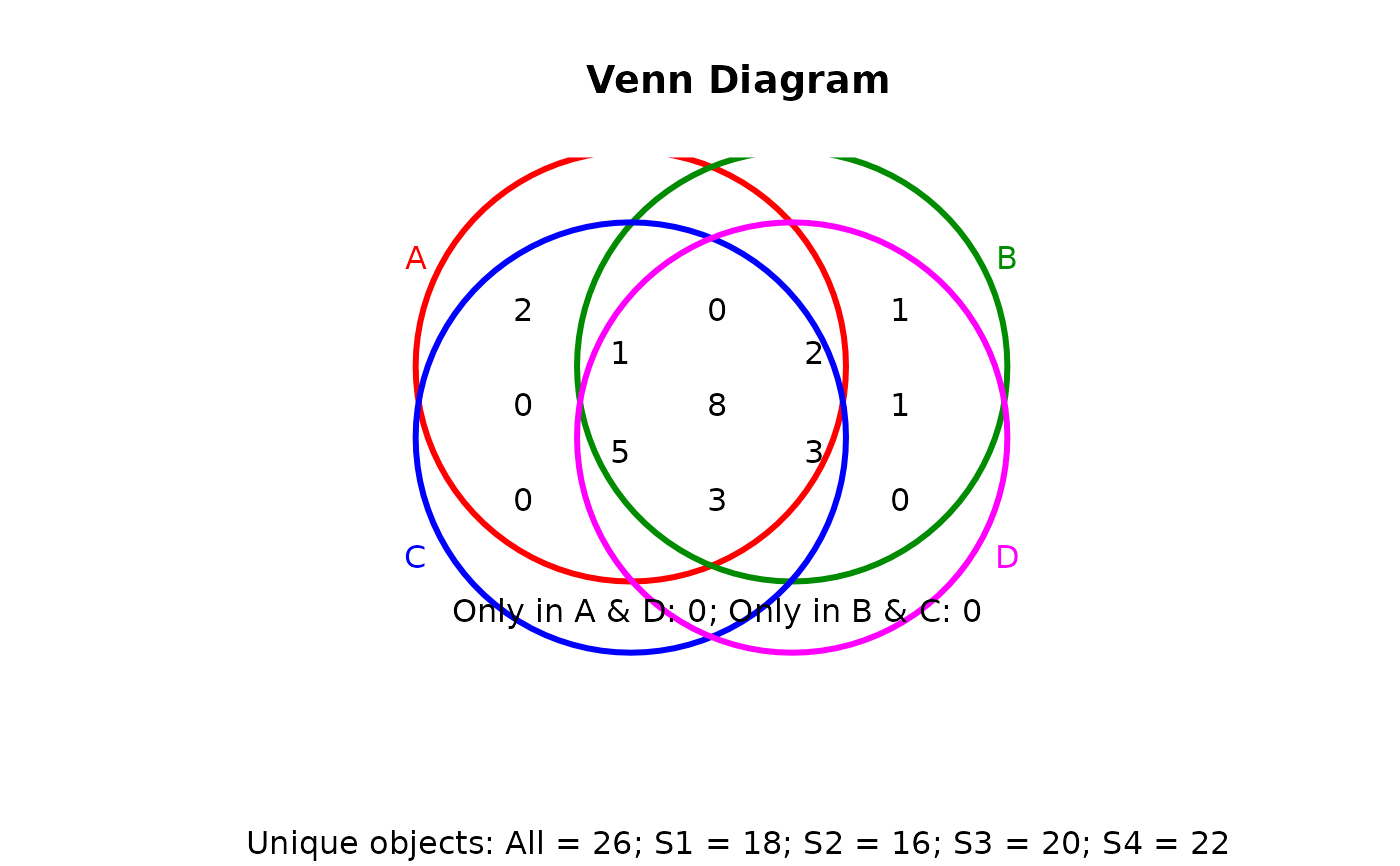
 ## Pseudo 4-way Venn diagram with circles
vennPlot(vennset, type="circle")
## Pseudo 4-way Venn diagram with circles
vennPlot(vennset, type="circle")
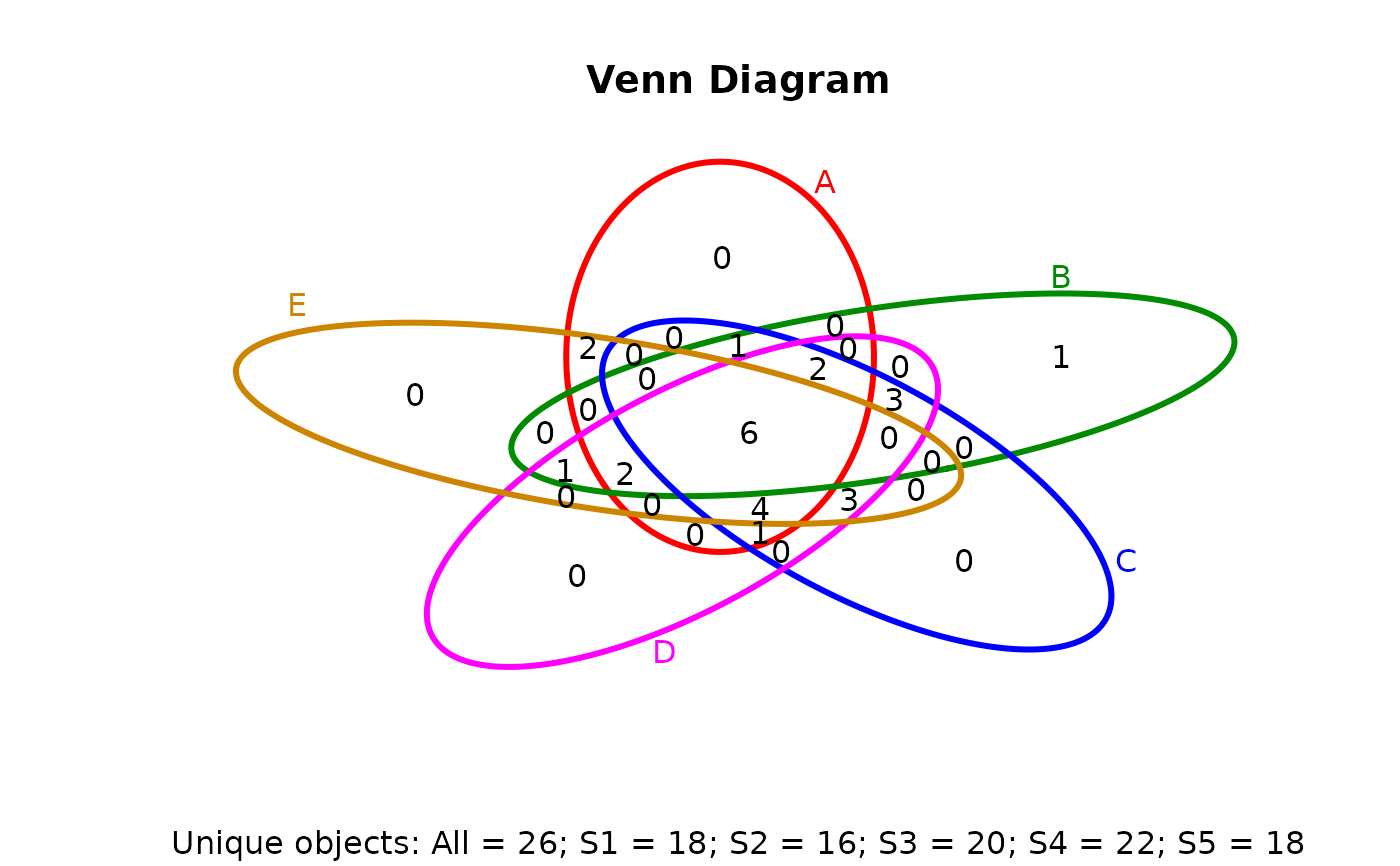
 ## 5-way Venn diagram
vennset <- overLapper(setlist[1:5], type="vennsets")
vennPlot(vennset)
## Alternative Venn count input to vennPlot (not recommended!)
counts <- sapply(vennlist(vennset), length)
vennPlot(counts)
## 5-way Venn diagram
vennset <- overLapper(setlist[1:5], type="vennsets")
vennPlot(vennset)
## Alternative Venn count input to vennPlot (not recommended!)
counts <- sapply(vennlist(vennset), length)
vennPlot(counts)
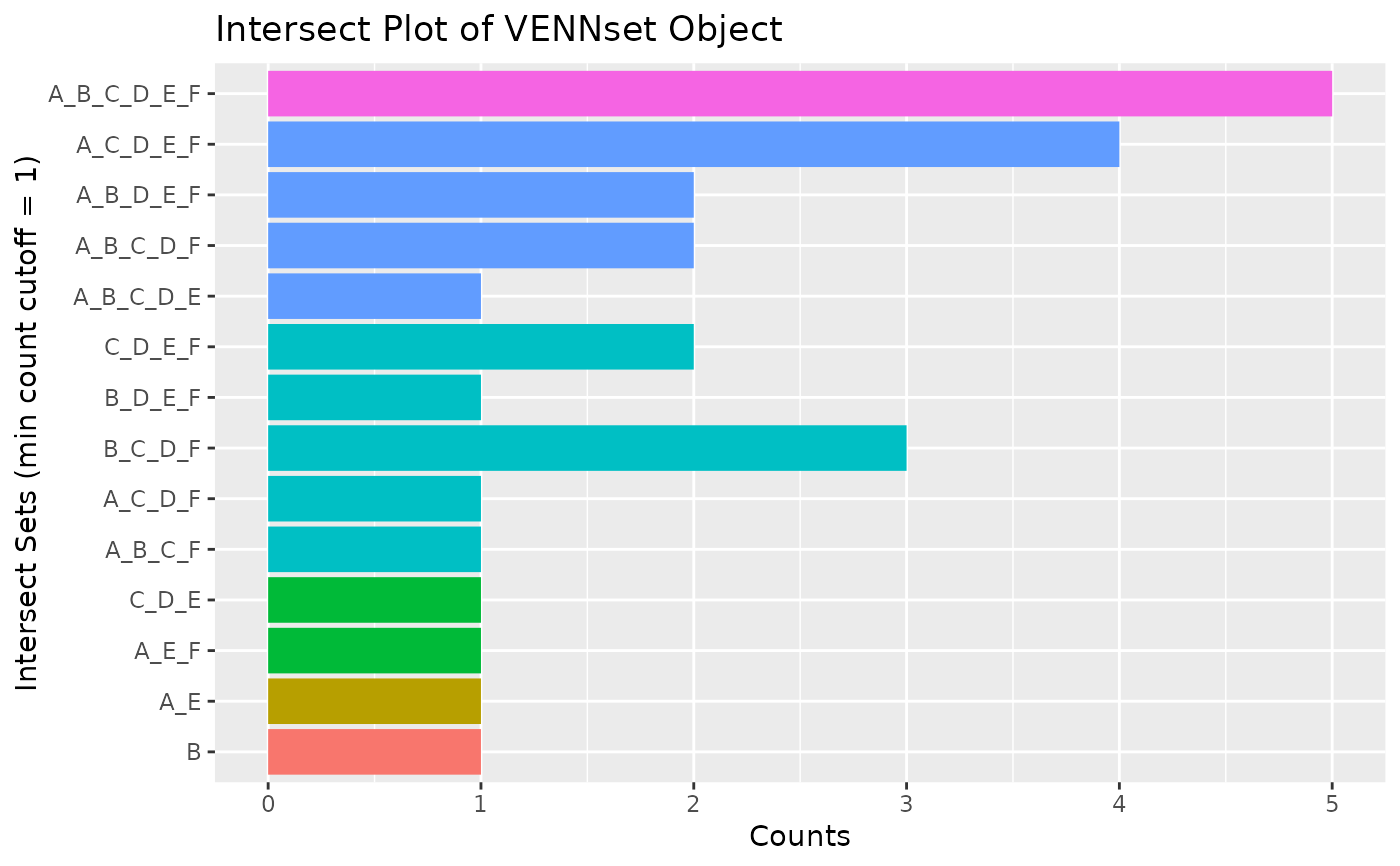
 ## 6-way Venn comparison as bar plot
vennset <- overLapper(setlist[1:6], type="vennsets")
olBarplot(vennset, mincount=1)
## 6-way Venn comparison as bar plot
vennset <- overLapper(setlist[1:6], type="vennsets")
olBarplot(vennset, mincount=1)
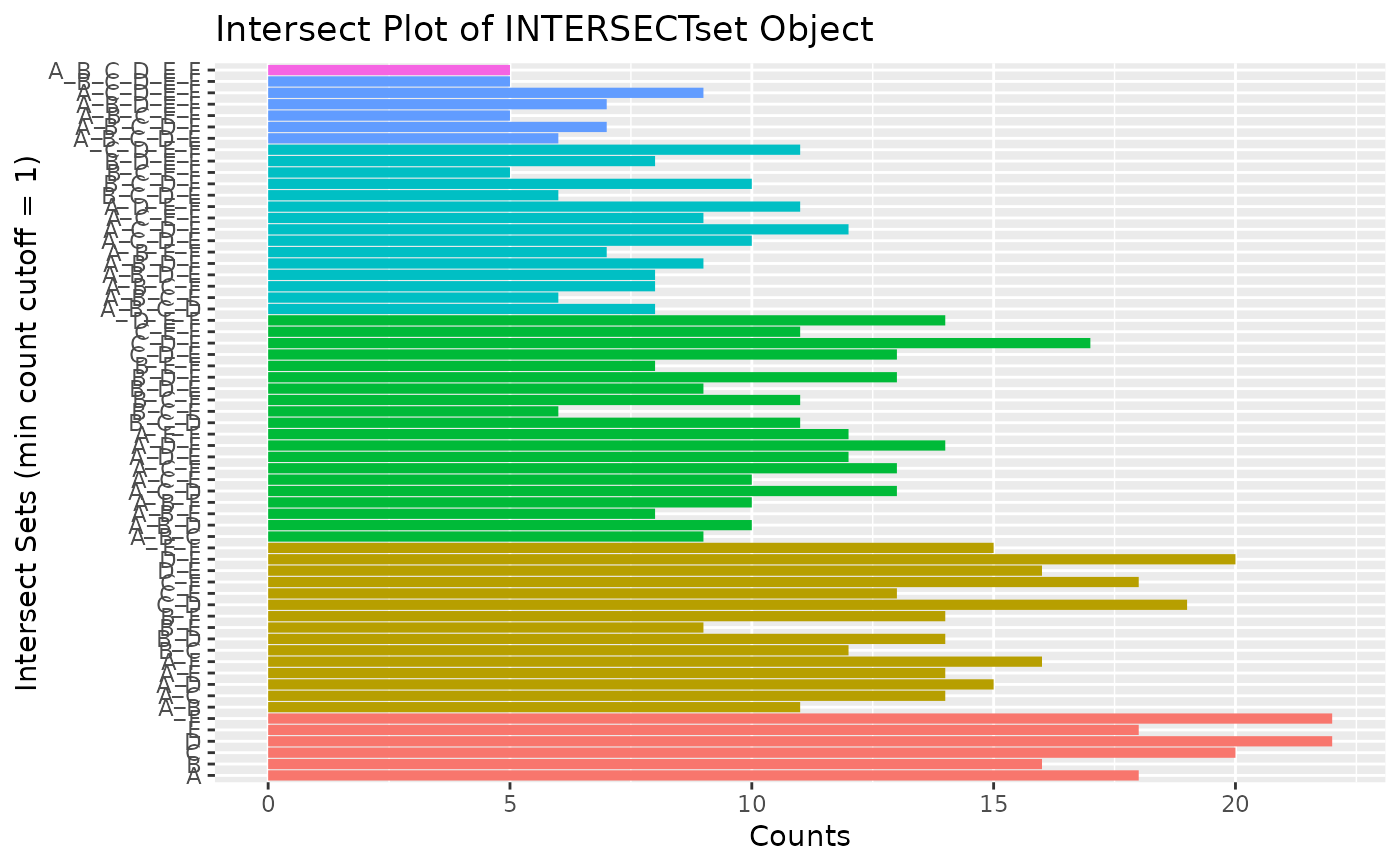
 ## Bar plot of standard intersect counts
interset <- overLapper(setlist, type="intersects")
olBarplot(interset, mincount=1)
## Bar plot of standard intersect counts
interset <- overLapper(setlist, type="intersects")
olBarplot(interset, mincount=1)
 ## Accessor methods for VENNset/INTERSECTset objects
names(vennset)
#> [1] "setlist" "intersectmatrix" "complexitylevels" "vennlist"
names(interset)
#> [1] "setlist" "intersectmatrix" "complexitylevels" "intersectlist"
setlist(vennset)
#> $A
#> [1] "a" "o" "z" "p" "s" "w" "k" "c" "n" "l" "i" "u" "r" "y" "e" "g" "m" "b"
#>
#> $B
#> [1] "s" "x" "l" "v" "i" "a" "f" "y" "r" "w" "d" "h" "b" "m" "o" "n"
#>
#> $C
#> [1] "s" "m" "f" "o" "k" "r" "j" "c" "e" "q" "l" "n" "d" "a" "v" "i" "u" "t" "g"
#> [20] "w"
#>
#> $D
#> [1] "f" "c" "u" "q" "d" "w" "j" "y" "t" "s" "l" "o" "x" "b" "a" "v" "e" "m" "k"
#> [20] "i" "n" "g"
#>
#> $E
#> [1] "t" "g" "p" "i" "a" "e" "b" "u" "j" "q" "x" "m" "c" "w" "s" "y" "l" "z"
#>
#> $F
#> [1] "s" "z" "k" "u" "c" "f" "r" "v" "o" "w" "y" "x" "q" "j" "b" "m" "n" "d" "e"
#> [20] "g" "a" "l"
#>
intersectmatrix(vennset)
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
complexitylevels(vennset)
#> [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
vennlist(vennset)
#> $A
#> character(0)
#>
#> $B
#> [1] "h"
#>
#> $C
#> character(0)
#>
#> $D
#> character(0)
#>
#> $E
#> character(0)
#>
#> $F
#> character(0)
#>
#> $A_B
#> character(0)
#>
#> $A_C
#> character(0)
#>
#> $A_D
#> character(0)
#>
#> $A_E
#> [1] "p"
#>
#> $A_F
#> character(0)
#>
#> $B_C
#> character(0)
#>
#> $B_D
#> character(0)
#>
#> $B_E
#> character(0)
#>
#> $B_F
#> character(0)
#>
#> $C_D
#> character(0)
#>
#> $C_E
#> character(0)
#>
#> $C_F
#> character(0)
#>
#> $D_E
#> character(0)
#>
#> $D_F
#> character(0)
#>
#> $E_F
#> character(0)
#>
#> $A_B_C
#> character(0)
#>
#> $A_B_D
#> character(0)
#>
#> $A_B_E
#> character(0)
#>
#> $A_B_F
#> character(0)
#>
#> $A_C_D
#> character(0)
#>
#> $A_C_E
#> character(0)
#>
#> $A_C_F
#> character(0)
#>
#> $A_D_E
#> character(0)
#>
#> $A_D_F
#> character(0)
#>
#> $A_E_F
#> [1] "z"
#>
#> $B_C_D
#> character(0)
#>
#> $B_C_E
#> character(0)
#>
#> $B_C_F
#> character(0)
#>
#> $B_D_E
#> character(0)
#>
#> $B_D_F
#> character(0)
#>
#> $B_E_F
#> character(0)
#>
#> $C_D_E
#> [1] "t"
#>
#> $C_D_F
#> character(0)
#>
#> $C_E_F
#> character(0)
#>
#> $D_E_F
#> character(0)
#>
#> $A_B_C_D
#> character(0)
#>
#> $A_B_C_E
#> character(0)
#>
#> $A_B_C_F
#> [1] "r"
#>
#> $A_B_D_E
#> character(0)
#>
#> $A_B_D_F
#> character(0)
#>
#> $A_B_E_F
#> character(0)
#>
#> $A_C_D_E
#> character(0)
#>
#> $A_C_D_F
#> [1] "k"
#>
#> $A_C_E_F
#> character(0)
#>
#> $A_D_E_F
#> character(0)
#>
#> $B_C_D_E
#> character(0)
#>
#> $B_C_D_F
#> [1] "d" "f" "v"
#>
#> $B_C_E_F
#> character(0)
#>
#> $B_D_E_F
#> [1] "x"
#>
#> $C_D_E_F
#> [1] "j" "q"
#>
#> $A_B_C_D_E
#> [1] "i"
#>
#> $A_B_C_D_F
#> [1] "n" "o"
#>
#> $A_B_C_E_F
#> character(0)
#>
#> $A_B_D_E_F
#> [1] "b" "y"
#>
#> $A_C_D_E_F
#> [1] "c" "e" "g" "u"
#>
#> $B_C_D_E_F
#> character(0)
#>
#> $A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
intersectlist(interset)
#> $A
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "p" "r" "s" "u" "w" "y" "z"
#>
#> $B
#> [1] "a" "b" "d" "f" "h" "i" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $C
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "r" "s" "t" "u" "v"
#> [20] "w"
#>
#> $D
#> [1] "a" "b" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v"
#> [20] "w" "x" "y"
#>
#> $E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "p" "q" "s" "t" "u" "w" "x" "y" "z"
#>
#> $F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#> [20] "x" "y" "z"
#>
#> $A_B
#> [1] "a" "b" "i" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $A_C
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $A_D
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $A_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "p" "s" "u" "w" "y" "z"
#>
#> $A_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w" "y" "z"
#>
#> $B_C
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $B_D
#> [1] "a" "b" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $B_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $C_D
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v" "w"
#>
#> $C_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $C_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#>
#> $D_E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w" "x" "y"
#>
#> $D_F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w" "x"
#> [20] "y"
#>
#> $E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y" "z"
#>
#> $A_B_C
#> [1] "a" "i" "l" "m" "n" "o" "r" "s" "w"
#>
#> $A_B_D
#> [1] "a" "b" "i" "l" "m" "n" "o" "s" "w" "y"
#>
#> $A_B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $A_B_F
#> [1] "a" "b" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $A_C_D
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $A_C_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $A_C_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $A_D_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "s" "u" "w" "y"
#>
#> $A_D_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $A_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y" "z"
#>
#> $B_C_D
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w"
#>
#> $B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $B_C_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $B_D_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $C_D_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $C_D_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w"
#>
#> $C_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $D_E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y"
#>
#> $A_B_C_D
#> [1] "a" "i" "l" "m" "n" "o" "s" "w"
#>
#> $A_B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $A_B_C_F
#> [1] "a" "l" "m" "n" "o" "r" "s" "w"
#>
#> $A_B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $A_B_D_F
#> [1] "a" "b" "l" "m" "n" "o" "s" "w" "y"
#>
#> $A_B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $A_C_D_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $A_C_D_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $A_C_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $A_D_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y"
#>
#> $B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $B_C_D_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "s" "v" "w"
#>
#> $B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $C_D_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $A_B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $A_B_C_D_F
#> [1] "a" "l" "m" "n" "o" "s" "w"
#>
#> $A_B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $A_B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $A_C_D_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
## Coerce VENNset/INTERSECTset object to list
as.list(vennset)
#> $setlist
#> $setlist$A
#> [1] "a" "o" "z" "p" "s" "w" "k" "c" "n" "l" "i" "u" "r" "y" "e" "g" "m" "b"
#>
#> $setlist$B
#> [1] "s" "x" "l" "v" "i" "a" "f" "y" "r" "w" "d" "h" "b" "m" "o" "n"
#>
#> $setlist$C
#> [1] "s" "m" "f" "o" "k" "r" "j" "c" "e" "q" "l" "n" "d" "a" "v" "i" "u" "t" "g"
#> [20] "w"
#>
#> $setlist$D
#> [1] "f" "c" "u" "q" "d" "w" "j" "y" "t" "s" "l" "o" "x" "b" "a" "v" "e" "m" "k"
#> [20] "i" "n" "g"
#>
#> $setlist$E
#> [1] "t" "g" "p" "i" "a" "e" "b" "u" "j" "q" "x" "m" "c" "w" "s" "y" "l" "z"
#>
#> $setlist$F
#> [1] "s" "z" "k" "u" "c" "f" "r" "v" "o" "w" "y" "x" "q" "j" "b" "m" "n" "d" "e"
#> [20] "g" "a" "l"
#>
#>
#> $intersectmatrix
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
#>
#> $complexitylevels
#> [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
#>
#> $vennlist
#> $vennlist$A
#> character(0)
#>
#> $vennlist$B
#> [1] "h"
#>
#> $vennlist$C
#> character(0)
#>
#> $vennlist$D
#> character(0)
#>
#> $vennlist$E
#> character(0)
#>
#> $vennlist$F
#> character(0)
#>
#> $vennlist$A_B
#> character(0)
#>
#> $vennlist$A_C
#> character(0)
#>
#> $vennlist$A_D
#> character(0)
#>
#> $vennlist$A_E
#> [1] "p"
#>
#> $vennlist$A_F
#> character(0)
#>
#> $vennlist$B_C
#> character(0)
#>
#> $vennlist$B_D
#> character(0)
#>
#> $vennlist$B_E
#> character(0)
#>
#> $vennlist$B_F
#> character(0)
#>
#> $vennlist$C_D
#> character(0)
#>
#> $vennlist$C_E
#> character(0)
#>
#> $vennlist$C_F
#> character(0)
#>
#> $vennlist$D_E
#> character(0)
#>
#> $vennlist$D_F
#> character(0)
#>
#> $vennlist$E_F
#> character(0)
#>
#> $vennlist$A_B_C
#> character(0)
#>
#> $vennlist$A_B_D
#> character(0)
#>
#> $vennlist$A_B_E
#> character(0)
#>
#> $vennlist$A_B_F
#> character(0)
#>
#> $vennlist$A_C_D
#> character(0)
#>
#> $vennlist$A_C_E
#> character(0)
#>
#> $vennlist$A_C_F
#> character(0)
#>
#> $vennlist$A_D_E
#> character(0)
#>
#> $vennlist$A_D_F
#> character(0)
#>
#> $vennlist$A_E_F
#> [1] "z"
#>
#> $vennlist$B_C_D
#> character(0)
#>
#> $vennlist$B_C_E
#> character(0)
#>
#> $vennlist$B_C_F
#> character(0)
#>
#> $vennlist$B_D_E
#> character(0)
#>
#> $vennlist$B_D_F
#> character(0)
#>
#> $vennlist$B_E_F
#> character(0)
#>
#> $vennlist$C_D_E
#> [1] "t"
#>
#> $vennlist$C_D_F
#> character(0)
#>
#> $vennlist$C_E_F
#> character(0)
#>
#> $vennlist$D_E_F
#> character(0)
#>
#> $vennlist$A_B_C_D
#> character(0)
#>
#> $vennlist$A_B_C_E
#> character(0)
#>
#> $vennlist$A_B_C_F
#> [1] "r"
#>
#> $vennlist$A_B_D_E
#> character(0)
#>
#> $vennlist$A_B_D_F
#> character(0)
#>
#> $vennlist$A_B_E_F
#> character(0)
#>
#> $vennlist$A_C_D_E
#> character(0)
#>
#> $vennlist$A_C_D_F
#> [1] "k"
#>
#> $vennlist$A_C_E_F
#> character(0)
#>
#> $vennlist$A_D_E_F
#> character(0)
#>
#> $vennlist$B_C_D_E
#> character(0)
#>
#> $vennlist$B_C_D_F
#> [1] "d" "f" "v"
#>
#> $vennlist$B_C_E_F
#> character(0)
#>
#> $vennlist$B_D_E_F
#> [1] "x"
#>
#> $vennlist$C_D_E_F
#> [1] "j" "q"
#>
#> $vennlist$A_B_C_D_E
#> [1] "i"
#>
#> $vennlist$A_B_C_D_F
#> [1] "n" "o"
#>
#> $vennlist$A_B_C_E_F
#> character(0)
#>
#> $vennlist$A_B_D_E_F
#> [1] "b" "y"
#>
#> $vennlist$A_C_D_E_F
#> [1] "c" "e" "g" "u"
#>
#> $vennlist$B_C_D_E_F
#> character(0)
#>
#> $vennlist$A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#>
as.list(interset)
#> $setlist
#> $setlist$A
#> [1] "a" "o" "z" "p" "s" "w" "k" "c" "n" "l" "i" "u" "r" "y" "e" "g" "m" "b"
#>
#> $setlist$B
#> [1] "s" "x" "l" "v" "i" "a" "f" "y" "r" "w" "d" "h" "b" "m" "o" "n"
#>
#> $setlist$C
#> [1] "s" "m" "f" "o" "k" "r" "j" "c" "e" "q" "l" "n" "d" "a" "v" "i" "u" "t" "g"
#> [20] "w"
#>
#> $setlist$D
#> [1] "f" "c" "u" "q" "d" "w" "j" "y" "t" "s" "l" "o" "x" "b" "a" "v" "e" "m" "k"
#> [20] "i" "n" "g"
#>
#> $setlist$E
#> [1] "t" "g" "p" "i" "a" "e" "b" "u" "j" "q" "x" "m" "c" "w" "s" "y" "l" "z"
#>
#> $setlist$F
#> [1] "s" "z" "k" "u" "c" "f" "r" "v" "o" "w" "y" "x" "q" "j" "b" "m" "n" "d" "e"
#> [20] "g" "a" "l"
#>
#>
#> $intersectmatrix
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
#>
#> $complexitylevels
#> [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
#>
#> $intersectlist
#> $intersectlist$A
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "p" "r" "s" "u" "w" "y" "z"
#>
#> $intersectlist$B
#> [1] "a" "b" "d" "f" "h" "i" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $intersectlist$C
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "r" "s" "t" "u" "v"
#> [20] "w"
#>
#> $intersectlist$D
#> [1] "a" "b" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v"
#> [20] "w" "x" "y"
#>
#> $intersectlist$E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "p" "q" "s" "t" "u" "w" "x" "y" "z"
#>
#> $intersectlist$F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#> [20] "x" "y" "z"
#>
#> $intersectlist$A_B
#> [1] "a" "b" "i" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $intersectlist$A_C
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $intersectlist$A_D
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $intersectlist$A_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "p" "s" "u" "w" "y" "z"
#>
#> $intersectlist$A_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w" "y" "z"
#>
#> $intersectlist$B_C
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $intersectlist$B_D
#> [1] "a" "b" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $intersectlist$B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$B_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $intersectlist$C_D
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v" "w"
#>
#> $intersectlist$C_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $intersectlist$C_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#>
#> $intersectlist$D_E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w" "x" "y"
#>
#> $intersectlist$D_F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w" "x"
#> [20] "y"
#>
#> $intersectlist$E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y" "z"
#>
#> $intersectlist$A_B_C
#> [1] "a" "i" "l" "m" "n" "o" "r" "s" "w"
#>
#> $intersectlist$A_B_D
#> [1] "a" "b" "i" "l" "m" "n" "o" "s" "w" "y"
#>
#> $intersectlist$A_B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_B_F
#> [1] "a" "b" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $intersectlist$A_C_D
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $intersectlist$A_C_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $intersectlist$A_C_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $intersectlist$A_D_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "s" "u" "w" "y"
#>
#> $intersectlist$A_D_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $intersectlist$A_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y" "z"
#>
#> $intersectlist$B_C_D
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w"
#>
#> $intersectlist$B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$B_C_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $intersectlist$B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$B_D_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $intersectlist$B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$C_D_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $intersectlist$C_D_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w"
#>
#> $intersectlist$C_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $intersectlist$D_E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y"
#>
#> $intersectlist$A_B_C_D
#> [1] "a" "i" "l" "m" "n" "o" "s" "w"
#>
#> $intersectlist$A_B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_C_F
#> [1] "a" "l" "m" "n" "o" "r" "s" "w"
#>
#> $intersectlist$A_B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_B_D_F
#> [1] "a" "b" "l" "m" "n" "o" "s" "w" "y"
#>
#> $intersectlist$A_B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_C_D_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $intersectlist$A_C_D_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $intersectlist$A_C_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $intersectlist$A_D_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y"
#>
#> $intersectlist$B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$B_C_D_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "s" "v" "w"
#>
#> $intersectlist$B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $intersectlist$B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$C_D_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $intersectlist$A_B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_C_D_F
#> [1] "a" "l" "m" "n" "o" "s" "w"
#>
#> $intersectlist$A_B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_C_D_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $intersectlist$B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#>
## Pairwise intersect matrix and heatmap
olMA <- sapply(names(setlist),
function(x) sapply(names(setlist),
function(y) sum(setlist[[x]] %in% setlist[[y]])))
olMA
#> A B C D E F
#> A 18 11 14 15 14 16
#> B 11 16 12 14 9 14
#> C 14 12 20 19 13 18
#> D 15 14 19 22 16 20
#> E 14 9 13 16 18 15
#> F 16 14 18 20 15 22
heatmap(olMA, Rowv=NA, Colv=NA)
## Accessor methods for VENNset/INTERSECTset objects
names(vennset)
#> [1] "setlist" "intersectmatrix" "complexitylevels" "vennlist"
names(interset)
#> [1] "setlist" "intersectmatrix" "complexitylevels" "intersectlist"
setlist(vennset)
#> $A
#> [1] "a" "o" "z" "p" "s" "w" "k" "c" "n" "l" "i" "u" "r" "y" "e" "g" "m" "b"
#>
#> $B
#> [1] "s" "x" "l" "v" "i" "a" "f" "y" "r" "w" "d" "h" "b" "m" "o" "n"
#>
#> $C
#> [1] "s" "m" "f" "o" "k" "r" "j" "c" "e" "q" "l" "n" "d" "a" "v" "i" "u" "t" "g"
#> [20] "w"
#>
#> $D
#> [1] "f" "c" "u" "q" "d" "w" "j" "y" "t" "s" "l" "o" "x" "b" "a" "v" "e" "m" "k"
#> [20] "i" "n" "g"
#>
#> $E
#> [1] "t" "g" "p" "i" "a" "e" "b" "u" "j" "q" "x" "m" "c" "w" "s" "y" "l" "z"
#>
#> $F
#> [1] "s" "z" "k" "u" "c" "f" "r" "v" "o" "w" "y" "x" "q" "j" "b" "m" "n" "d" "e"
#> [20] "g" "a" "l"
#>
intersectmatrix(vennset)
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
complexitylevels(vennset)
#> [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
vennlist(vennset)
#> $A
#> character(0)
#>
#> $B
#> [1] "h"
#>
#> $C
#> character(0)
#>
#> $D
#> character(0)
#>
#> $E
#> character(0)
#>
#> $F
#> character(0)
#>
#> $A_B
#> character(0)
#>
#> $A_C
#> character(0)
#>
#> $A_D
#> character(0)
#>
#> $A_E
#> [1] "p"
#>
#> $A_F
#> character(0)
#>
#> $B_C
#> character(0)
#>
#> $B_D
#> character(0)
#>
#> $B_E
#> character(0)
#>
#> $B_F
#> character(0)
#>
#> $C_D
#> character(0)
#>
#> $C_E
#> character(0)
#>
#> $C_F
#> character(0)
#>
#> $D_E
#> character(0)
#>
#> $D_F
#> character(0)
#>
#> $E_F
#> character(0)
#>
#> $A_B_C
#> character(0)
#>
#> $A_B_D
#> character(0)
#>
#> $A_B_E
#> character(0)
#>
#> $A_B_F
#> character(0)
#>
#> $A_C_D
#> character(0)
#>
#> $A_C_E
#> character(0)
#>
#> $A_C_F
#> character(0)
#>
#> $A_D_E
#> character(0)
#>
#> $A_D_F
#> character(0)
#>
#> $A_E_F
#> [1] "z"
#>
#> $B_C_D
#> character(0)
#>
#> $B_C_E
#> character(0)
#>
#> $B_C_F
#> character(0)
#>
#> $B_D_E
#> character(0)
#>
#> $B_D_F
#> character(0)
#>
#> $B_E_F
#> character(0)
#>
#> $C_D_E
#> [1] "t"
#>
#> $C_D_F
#> character(0)
#>
#> $C_E_F
#> character(0)
#>
#> $D_E_F
#> character(0)
#>
#> $A_B_C_D
#> character(0)
#>
#> $A_B_C_E
#> character(0)
#>
#> $A_B_C_F
#> [1] "r"
#>
#> $A_B_D_E
#> character(0)
#>
#> $A_B_D_F
#> character(0)
#>
#> $A_B_E_F
#> character(0)
#>
#> $A_C_D_E
#> character(0)
#>
#> $A_C_D_F
#> [1] "k"
#>
#> $A_C_E_F
#> character(0)
#>
#> $A_D_E_F
#> character(0)
#>
#> $B_C_D_E
#> character(0)
#>
#> $B_C_D_F
#> [1] "d" "f" "v"
#>
#> $B_C_E_F
#> character(0)
#>
#> $B_D_E_F
#> [1] "x"
#>
#> $C_D_E_F
#> [1] "j" "q"
#>
#> $A_B_C_D_E
#> [1] "i"
#>
#> $A_B_C_D_F
#> [1] "n" "o"
#>
#> $A_B_C_E_F
#> character(0)
#>
#> $A_B_D_E_F
#> [1] "b" "y"
#>
#> $A_C_D_E_F
#> [1] "c" "e" "g" "u"
#>
#> $B_C_D_E_F
#> character(0)
#>
#> $A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
intersectlist(interset)
#> $A
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "p" "r" "s" "u" "w" "y" "z"
#>
#> $B
#> [1] "a" "b" "d" "f" "h" "i" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $C
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "r" "s" "t" "u" "v"
#> [20] "w"
#>
#> $D
#> [1] "a" "b" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v"
#> [20] "w" "x" "y"
#>
#> $E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "p" "q" "s" "t" "u" "w" "x" "y" "z"
#>
#> $F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#> [20] "x" "y" "z"
#>
#> $A_B
#> [1] "a" "b" "i" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $A_C
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $A_D
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $A_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "p" "s" "u" "w" "y" "z"
#>
#> $A_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w" "y" "z"
#>
#> $B_C
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $B_D
#> [1] "a" "b" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $B_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $C_D
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v" "w"
#>
#> $C_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $C_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#>
#> $D_E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w" "x" "y"
#>
#> $D_F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w" "x"
#> [20] "y"
#>
#> $E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y" "z"
#>
#> $A_B_C
#> [1] "a" "i" "l" "m" "n" "o" "r" "s" "w"
#>
#> $A_B_D
#> [1] "a" "b" "i" "l" "m" "n" "o" "s" "w" "y"
#>
#> $A_B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $A_B_F
#> [1] "a" "b" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $A_C_D
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $A_C_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $A_C_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $A_D_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "s" "u" "w" "y"
#>
#> $A_D_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $A_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y" "z"
#>
#> $B_C_D
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w"
#>
#> $B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $B_C_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $B_D_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $C_D_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $C_D_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w"
#>
#> $C_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $D_E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y"
#>
#> $A_B_C_D
#> [1] "a" "i" "l" "m" "n" "o" "s" "w"
#>
#> $A_B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $A_B_C_F
#> [1] "a" "l" "m" "n" "o" "r" "s" "w"
#>
#> $A_B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $A_B_D_F
#> [1] "a" "b" "l" "m" "n" "o" "s" "w" "y"
#>
#> $A_B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $A_C_D_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $A_C_D_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $A_C_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $A_D_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y"
#>
#> $B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $B_C_D_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "s" "v" "w"
#>
#> $B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $C_D_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $A_B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $A_B_C_D_F
#> [1] "a" "l" "m" "n" "o" "s" "w"
#>
#> $A_B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $A_B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $A_C_D_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
## Coerce VENNset/INTERSECTset object to list
as.list(vennset)
#> $setlist
#> $setlist$A
#> [1] "a" "o" "z" "p" "s" "w" "k" "c" "n" "l" "i" "u" "r" "y" "e" "g" "m" "b"
#>
#> $setlist$B
#> [1] "s" "x" "l" "v" "i" "a" "f" "y" "r" "w" "d" "h" "b" "m" "o" "n"
#>
#> $setlist$C
#> [1] "s" "m" "f" "o" "k" "r" "j" "c" "e" "q" "l" "n" "d" "a" "v" "i" "u" "t" "g"
#> [20] "w"
#>
#> $setlist$D
#> [1] "f" "c" "u" "q" "d" "w" "j" "y" "t" "s" "l" "o" "x" "b" "a" "v" "e" "m" "k"
#> [20] "i" "n" "g"
#>
#> $setlist$E
#> [1] "t" "g" "p" "i" "a" "e" "b" "u" "j" "q" "x" "m" "c" "w" "s" "y" "l" "z"
#>
#> $setlist$F
#> [1] "s" "z" "k" "u" "c" "f" "r" "v" "o" "w" "y" "x" "q" "j" "b" "m" "n" "d" "e"
#> [20] "g" "a" "l"
#>
#>
#> $intersectmatrix
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
#>
#> $complexitylevels
#> [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
#>
#> $vennlist
#> $vennlist$A
#> character(0)
#>
#> $vennlist$B
#> [1] "h"
#>
#> $vennlist$C
#> character(0)
#>
#> $vennlist$D
#> character(0)
#>
#> $vennlist$E
#> character(0)
#>
#> $vennlist$F
#> character(0)
#>
#> $vennlist$A_B
#> character(0)
#>
#> $vennlist$A_C
#> character(0)
#>
#> $vennlist$A_D
#> character(0)
#>
#> $vennlist$A_E
#> [1] "p"
#>
#> $vennlist$A_F
#> character(0)
#>
#> $vennlist$B_C
#> character(0)
#>
#> $vennlist$B_D
#> character(0)
#>
#> $vennlist$B_E
#> character(0)
#>
#> $vennlist$B_F
#> character(0)
#>
#> $vennlist$C_D
#> character(0)
#>
#> $vennlist$C_E
#> character(0)
#>
#> $vennlist$C_F
#> character(0)
#>
#> $vennlist$D_E
#> character(0)
#>
#> $vennlist$D_F
#> character(0)
#>
#> $vennlist$E_F
#> character(0)
#>
#> $vennlist$A_B_C
#> character(0)
#>
#> $vennlist$A_B_D
#> character(0)
#>
#> $vennlist$A_B_E
#> character(0)
#>
#> $vennlist$A_B_F
#> character(0)
#>
#> $vennlist$A_C_D
#> character(0)
#>
#> $vennlist$A_C_E
#> character(0)
#>
#> $vennlist$A_C_F
#> character(0)
#>
#> $vennlist$A_D_E
#> character(0)
#>
#> $vennlist$A_D_F
#> character(0)
#>
#> $vennlist$A_E_F
#> [1] "z"
#>
#> $vennlist$B_C_D
#> character(0)
#>
#> $vennlist$B_C_E
#> character(0)
#>
#> $vennlist$B_C_F
#> character(0)
#>
#> $vennlist$B_D_E
#> character(0)
#>
#> $vennlist$B_D_F
#> character(0)
#>
#> $vennlist$B_E_F
#> character(0)
#>
#> $vennlist$C_D_E
#> [1] "t"
#>
#> $vennlist$C_D_F
#> character(0)
#>
#> $vennlist$C_E_F
#> character(0)
#>
#> $vennlist$D_E_F
#> character(0)
#>
#> $vennlist$A_B_C_D
#> character(0)
#>
#> $vennlist$A_B_C_E
#> character(0)
#>
#> $vennlist$A_B_C_F
#> [1] "r"
#>
#> $vennlist$A_B_D_E
#> character(0)
#>
#> $vennlist$A_B_D_F
#> character(0)
#>
#> $vennlist$A_B_E_F
#> character(0)
#>
#> $vennlist$A_C_D_E
#> character(0)
#>
#> $vennlist$A_C_D_F
#> [1] "k"
#>
#> $vennlist$A_C_E_F
#> character(0)
#>
#> $vennlist$A_D_E_F
#> character(0)
#>
#> $vennlist$B_C_D_E
#> character(0)
#>
#> $vennlist$B_C_D_F
#> [1] "d" "f" "v"
#>
#> $vennlist$B_C_E_F
#> character(0)
#>
#> $vennlist$B_D_E_F
#> [1] "x"
#>
#> $vennlist$C_D_E_F
#> [1] "j" "q"
#>
#> $vennlist$A_B_C_D_E
#> [1] "i"
#>
#> $vennlist$A_B_C_D_F
#> [1] "n" "o"
#>
#> $vennlist$A_B_C_E_F
#> character(0)
#>
#> $vennlist$A_B_D_E_F
#> [1] "b" "y"
#>
#> $vennlist$A_C_D_E_F
#> [1] "c" "e" "g" "u"
#>
#> $vennlist$B_C_D_E_F
#> character(0)
#>
#> $vennlist$A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#>
as.list(interset)
#> $setlist
#> $setlist$A
#> [1] "a" "o" "z" "p" "s" "w" "k" "c" "n" "l" "i" "u" "r" "y" "e" "g" "m" "b"
#>
#> $setlist$B
#> [1] "s" "x" "l" "v" "i" "a" "f" "y" "r" "w" "d" "h" "b" "m" "o" "n"
#>
#> $setlist$C
#> [1] "s" "m" "f" "o" "k" "r" "j" "c" "e" "q" "l" "n" "d" "a" "v" "i" "u" "t" "g"
#> [20] "w"
#>
#> $setlist$D
#> [1] "f" "c" "u" "q" "d" "w" "j" "y" "t" "s" "l" "o" "x" "b" "a" "v" "e" "m" "k"
#> [20] "i" "n" "g"
#>
#> $setlist$E
#> [1] "t" "g" "p" "i" "a" "e" "b" "u" "j" "q" "x" "m" "c" "w" "s" "y" "l" "z"
#>
#> $setlist$F
#> [1] "s" "z" "k" "u" "c" "f" "r" "v" "o" "w" "y" "x" "q" "j" "b" "m" "n" "d" "e"
#> [20] "g" "a" "l"
#>
#>
#> $intersectmatrix
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
#>
#> $complexitylevels
#> [1] 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
#> [39] 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6
#>
#> $intersectlist
#> $intersectlist$A
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "p" "r" "s" "u" "w" "y" "z"
#>
#> $intersectlist$B
#> [1] "a" "b" "d" "f" "h" "i" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $intersectlist$C
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "r" "s" "t" "u" "v"
#> [20] "w"
#>
#> $intersectlist$D
#> [1] "a" "b" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v"
#> [20] "w" "x" "y"
#>
#> $intersectlist$E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "p" "q" "s" "t" "u" "w" "x" "y" "z"
#>
#> $intersectlist$F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#> [20] "x" "y" "z"
#>
#> $intersectlist$A_B
#> [1] "a" "b" "i" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $intersectlist$A_C
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $intersectlist$A_D
#> [1] "a" "b" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $intersectlist$A_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "p" "s" "u" "w" "y" "z"
#>
#> $intersectlist$A_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w" "y" "z"
#>
#> $intersectlist$B_C
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $intersectlist$B_D
#> [1] "a" "b" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $intersectlist$B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$B_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w" "x" "y"
#>
#> $intersectlist$C_D
#> [1] "a" "c" "d" "e" "f" "g" "i" "j" "k" "l" "m" "n" "o" "q" "s" "t" "u" "v" "w"
#>
#> $intersectlist$C_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $intersectlist$C_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "r" "s" "u" "v" "w"
#>
#> $intersectlist$D_E
#> [1] "a" "b" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w" "x" "y"
#>
#> $intersectlist$D_F
#> [1] "a" "b" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w" "x"
#> [20] "y"
#>
#> $intersectlist$E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y" "z"
#>
#> $intersectlist$A_B_C
#> [1] "a" "i" "l" "m" "n" "o" "r" "s" "w"
#>
#> $intersectlist$A_B_D
#> [1] "a" "b" "i" "l" "m" "n" "o" "s" "w" "y"
#>
#> $intersectlist$A_B_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_B_F
#> [1] "a" "b" "l" "m" "n" "o" "r" "s" "w" "y"
#>
#> $intersectlist$A_C_D
#> [1] "a" "c" "e" "g" "i" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $intersectlist$A_C_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $intersectlist$A_C_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "r" "s" "u" "w"
#>
#> $intersectlist$A_D_E
#> [1] "a" "b" "c" "e" "g" "i" "l" "m" "s" "u" "w" "y"
#>
#> $intersectlist$A_D_F
#> [1] "a" "b" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w" "y"
#>
#> $intersectlist$A_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y" "z"
#>
#> $intersectlist$B_C_D
#> [1] "a" "d" "f" "i" "l" "m" "n" "o" "s" "v" "w"
#>
#> $intersectlist$B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$B_C_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "r" "s" "v" "w"
#>
#> $intersectlist$B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$B_D_F
#> [1] "a" "b" "d" "f" "l" "m" "n" "o" "s" "v" "w" "x" "y"
#>
#> $intersectlist$B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$C_D_E
#> [1] "a" "c" "e" "g" "i" "j" "l" "m" "q" "s" "t" "u" "w"
#>
#> $intersectlist$C_D_F
#> [1] "a" "c" "d" "e" "f" "g" "j" "k" "l" "m" "n" "o" "q" "s" "u" "v" "w"
#>
#> $intersectlist$C_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $intersectlist$D_E_F
#> [1] "a" "b" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w" "x" "y"
#>
#> $intersectlist$A_B_C_D
#> [1] "a" "i" "l" "m" "n" "o" "s" "w"
#>
#> $intersectlist$A_B_C_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_C_F
#> [1] "a" "l" "m" "n" "o" "r" "s" "w"
#>
#> $intersectlist$A_B_D_E
#> [1] "a" "b" "i" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_B_D_F
#> [1] "a" "b" "l" "m" "n" "o" "s" "w" "y"
#>
#> $intersectlist$A_B_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_C_D_E
#> [1] "a" "c" "e" "g" "i" "l" "m" "s" "u" "w"
#>
#> $intersectlist$A_C_D_F
#> [1] "a" "c" "e" "g" "k" "l" "m" "n" "o" "s" "u" "w"
#>
#> $intersectlist$A_C_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $intersectlist$A_D_E_F
#> [1] "a" "b" "c" "e" "g" "l" "m" "s" "u" "w" "y"
#>
#> $intersectlist$B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$B_C_D_F
#> [1] "a" "d" "f" "l" "m" "n" "o" "s" "v" "w"
#>
#> $intersectlist$B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $intersectlist$B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "x" "y"
#>
#> $intersectlist$C_D_E_F
#> [1] "a" "c" "e" "g" "j" "l" "m" "q" "s" "u" "w"
#>
#> $intersectlist$A_B_C_D_E
#> [1] "a" "i" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_C_D_F
#> [1] "a" "l" "m" "n" "o" "s" "w"
#>
#> $intersectlist$A_B_C_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_D_E_F
#> [1] "a" "b" "l" "m" "s" "w" "y"
#>
#> $intersectlist$A_C_D_E_F
#> [1] "a" "c" "e" "g" "l" "m" "s" "u" "w"
#>
#> $intersectlist$B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#> $intersectlist$A_B_C_D_E_F
#> [1] "a" "l" "m" "s" "w"
#>
#>
## Pairwise intersect matrix and heatmap
olMA <- sapply(names(setlist),
function(x) sapply(names(setlist),
function(y) sum(setlist[[x]] %in% setlist[[y]])))
olMA
#> A B C D E F
#> A 18 11 14 15 14 16
#> B 11 16 12 14 9 14
#> C 14 12 20 19 13 18
#> D 15 14 19 22 16 20
#> E 14 9 13 16 18 15
#> F 16 14 18 20 15 22
heatmap(olMA, Rowv=NA, Colv=NA)
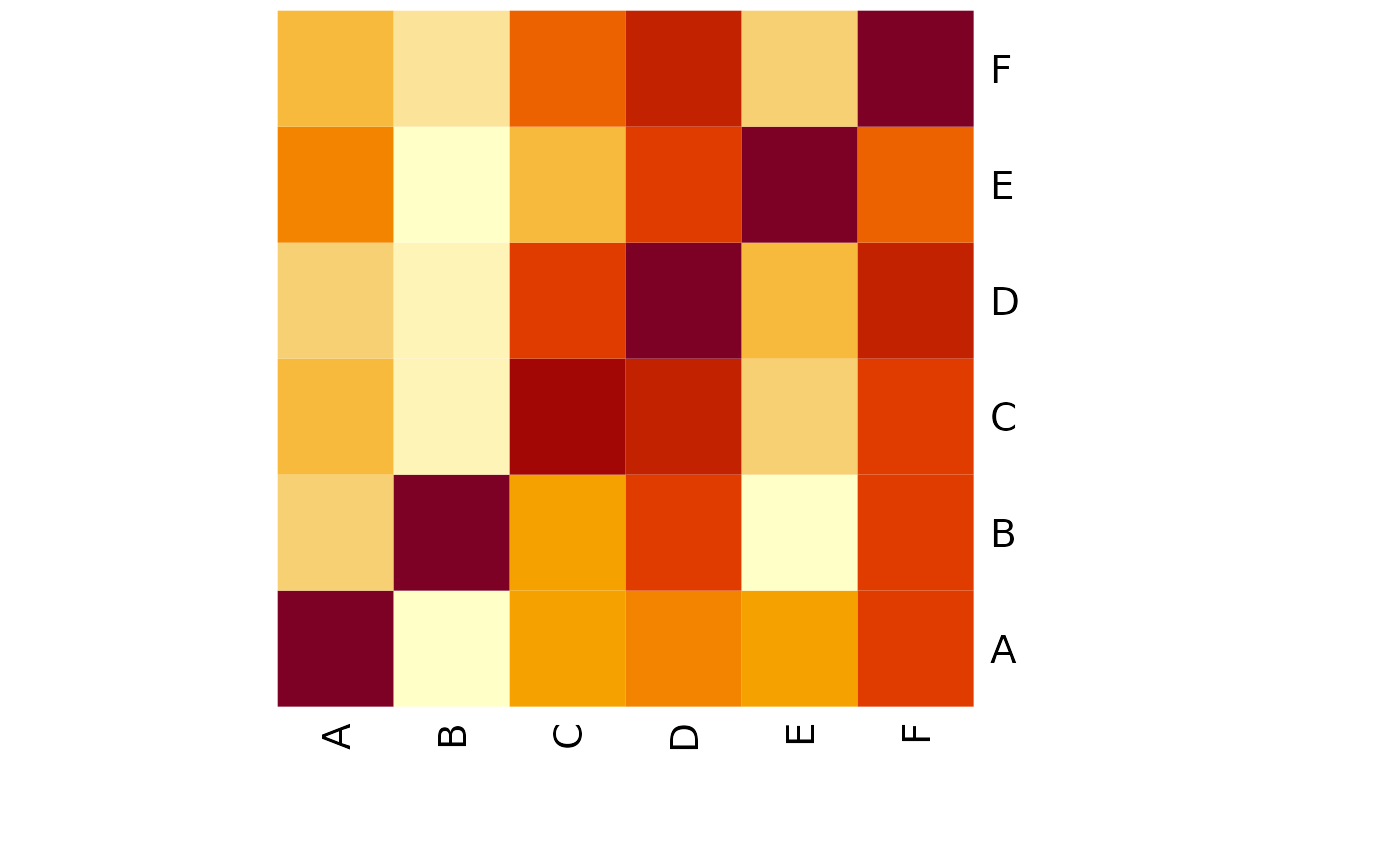 ## Presence-absence matrices for large numbers of sample sets
interset <- overLapper(setlist=setlist, type="intersects", complexity=2)
(paMA <- intersectmatrix(interset))
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
heatmap(paMA, Rowv=NA, Colv=NA, col=c("white", "gray"))
## Presence-absence matrices for large numbers of sample sets
interset <- overLapper(setlist=setlist, type="intersects", complexity=2)
(paMA <- intersectmatrix(interset))
#> A B C D E F
#> a 1 1 1 1 1 1
#> b 1 1 0 1 1 1
#> c 1 0 1 1 1 1
#> d 0 1 1 1 0 1
#> e 1 0 1 1 1 1
#> f 0 1 1 1 0 1
#> g 1 0 1 1 1 1
#> h 0 1 0 0 0 0
#> i 1 1 1 1 1 0
#> j 0 0 1 1 1 1
#> k 1 0 1 1 0 1
#> l 1 1 1 1 1 1
#> m 1 1 1 1 1 1
#> n 1 1 1 1 0 1
#> o 1 1 1 1 0 1
#> p 1 0 0 0 1 0
#> q 0 0 1 1 1 1
#> r 1 1 1 0 0 1
#> s 1 1 1 1 1 1
#> t 0 0 1 1 1 0
#> u 1 0 1 1 1 1
#> v 0 1 1 1 0 1
#> w 1 1 1 1 1 1
#> x 0 1 0 1 1 1
#> y 1 1 0 1 1 1
#> z 1 0 0 0 1 1
heatmap(paMA, Rowv=NA, Colv=NA, col=c("white", "gray"))
